Юрченко Борисович - Философия и логика времени

Если делить интервал времени до бесконечности, придав этой процедуре вид эффекта Доплера, то в пределе мы должны получить квант времени, равный нулю. Это и есть то настоящее, в котором Ахиллес догоняет черепаху. Если вернуться к аналогии с песочными часами, то наша цель измельчить песчинку до такого состояния, чтобы ее присутствие ничем не отличалось бы от ее отсутствия. Но сумма нулей, как уже говорилось, всегда равна нулю. А это и есть то, что Гегель определял как вечное настоящее. В физике это вечное настоящее, в котором нет времени и поэтому корреляции между двумя частицами происходят мгновенно, оказывается нелокальным миром, предсказанным ЭПР. Но наше самосознание и тождественный ему мир не могут существовать в таком состоянии. Мы живем в локальном релятивистском мире, где время движется, «набухает» по выражению Бергсона. А вместе с ним набухает, т.е. расширяется и наша Вселенная. И это пространственное расширение подобно обратному процессу деления временного интервала.

Это значит, что континуальный эфир лежит ниже границы математического анализа, на которой производится дифференцирование. В физическом смысле появление бесконечно малой величины равноценно появлению дискретного метрического пространства-времени. КМ говорит нам, что нижней границей этого пространства-времени является физический вакуум. Именно принцип неопределенности позволяет перейти от абсолютного покоя к движению, от нелокального мира к локальному. Благодаря этому принципу световая точка эфира становится точкой пространства-времени. В противном случае, как мы уже говорили, все в мире должно двигаться со скоростью света. Такая Вселенная не может существовать. Вакуум можно назвать буфером, который отделяет бытие от небытия.

Совершенно условно (а по-другому это, пожалуй, сделать нельзя) мы попробуем проиллюстрировать траекторию Ахиллеса в искаженном пространстве Минковского. Эта история становится историей другого мифического персонажа – Орфея, спускающегося в ад. В таком сюрреалистическом пространстве световой конус представлен сильно развернутым, чтобы как-то отделить его от физического пространства, хотя по сути они сливаются, делая подобными «застывшую» в мгновенном покое 3-мерную Вселенную и эфир, который мы представляем гиперплоскостью нулевой толщины. Ньютоновская модель была, можно сказать, инфантильной моделью эфира, в котором Вселенная логически невозможна. Она выстраивается над ним как класс страт M/t .

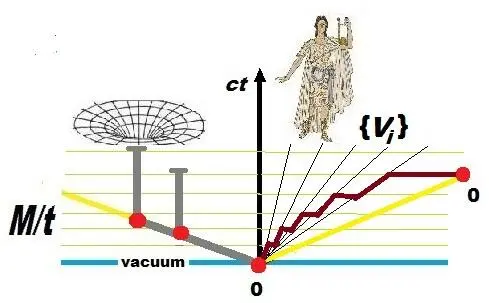
Рис.8

Также условно мы вынуждены выразить класс эквивалентностей ИСО/~, каждая из которых имеет собственную плотность времени с точностью до кванта времени и соответственно определенную энергию гравитационного поля, в котором метрический тензор не зависит от времени, образуя t-подобное поле Киллинга. Конечная подалгебра Ли этих полей должна распространяться и на плотности времени. Иначе говоря, класс ИСО/~ есть циклическая (коммутативная) группа плотностей, разложенных по степеням кванта времени с алгебраическим сложением по скоростям (ИСО) и групповым умножением по дифференциалам (плотности времени).

Геометрически этот класс составляет некий «бутон конусов» , каждый из которых состоит из мировых линий с квантовыми инерциальными метриками Бутон должен обладать странным свойством: , отражающим тот факт, что абсолютный покой в пространстве эквивалентен абсолютному покою во времени, поскольку в обоих случаях необходима скорость света, как это и подразумевается в преобразованиях Лоренца. Ахиллес, т.е. Орфей, в свободном падении при равномерном ускорении a = const приближаясь к границе конуса, приближается к нелокальному миру вечного настоящего. Сингулярность, в которую он попадает, ничем не отличается от сингулярности, лежащий в основании Вселенной.

Рекурсивная форма преобразований Лоренца, представленная выше формулой (4.4), подразумевает, что имеется восходящая через упорядоченное множество (квантовых) ИСО череда интервалов, которая начинается в эфире, релятивизуя его, по выражению Эйнштейна, в пространство-время. Математически инерциальные квантовые метрики соответствуют циклической группе дифференциалов , образующих класс канонических накрытий (покрытий) континуума , который сам является сингулярностью (эфиром):

В отличие от классического определения покрытия как объединения семейства множеств, включающего в себя данное множество, принятое здесь словоупотребление имеет иной смысл. В классе канонических покрытий, каждое из которых полностью покрывает континуум , данное множество является нижней границей: