Питер Макоуэн - Вычислительное мышление - Метод решения сложных задач

Теперь 7 >5, и на выходе 1, как нам и нужно: «Есть две монеты». И снова мы следуем правилу П1 и не делаем ничего.

Более того, если мы попробуем все четыре комбинации монет в щелях, то каждая из них даст правильный выход. Ура! Обучения не потребовалось. Но в данном случае нам повезло. Нам случайно сдали столько карт (три, четыре и пять), что машина сработала правильно. С таким количеством карт она всегда может правильно сказать, присутствуют две монеты или нет. Но что будет, если не повезет? Тогда придется играть по-другому и учиться необходимому поведению. Давайте рассмотрим другую игру.

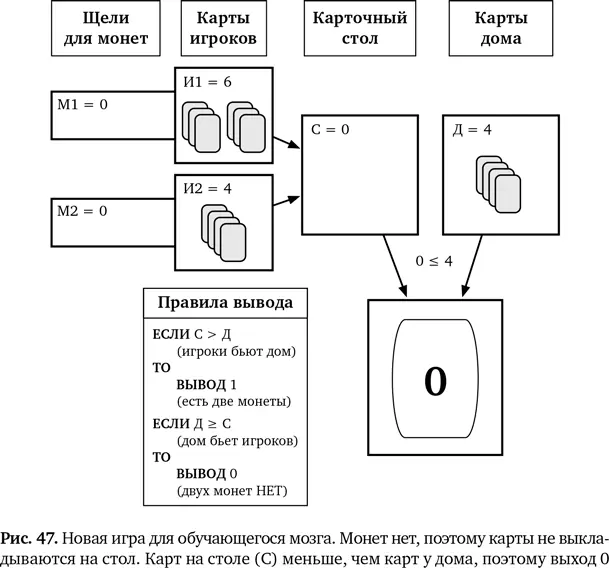
Мы снова начинаем с того, что произвольно сдаем игрокам и дому небольшое количество карт. На этот раз у игрока 1 на столе шесть карт, у игрока 2 — четыре карты, и у дома тоже четыре карты.

Ситуация, когда ни в одной щели нет монет, а значит, М1 и М2 равны 0, легкая. Карты не перемещаются, для дома мы получаем 0 <4, и на выходе 0: «Двух монет НЕТ». Условие (М1 ,М2) = (0 ,0) корректно. Это показано на рис. 47.

Если монета есть только в щели 2, значит, (М1 ,М2) = (0 ,1). Тогда карты игрока 2 идут вперед. Игрок 1 остается на месте, и на стол попадают четыре карты. На выходе мы имеем 0: «Двух монет НЕТ». Помните, что для получения 1 на выходе нам нужно, чтобы сумма карт на столе была больше (а не просто равна) Д. То есть ничего не меняется, и мы снова следуем правилу П1. Условие (М1 ,М2) = (0 ,1) корректно.

Теперь поместите одну монету в щель М1 и ни одной — в щель М2. И снова мы хотим получить на выходе 0, однако посмотрите на карты! На карточном столе у нас 6 ≥4, а значит, на выходе 1, и это неверно! Нужно применить правило П2. В нем говорится:

« ЕСЛИсыгранная партия дает на выходе 1, но мы хотели получить 0, чтобы это соответствовало таблице выходов,

ТОзаберите М1 карт у игрока 1 и М2 карт у игрока 2».

Это значит, что, поскольку М1 равно 1 и М2 равно 0, мы забираем карту у игрока 1, но не забираем у игрока 2. Новое значение И1 — 5 (6 −1), а И2 остается равно 4.

Забрав карту из стопки игрока 1, мы возвращаем его карты. Мы не забрали ни одной карты игрока 2. Машина начала учиться.

Теперь мы выбираем другое условие и пробуем еще раз. Экспериментируя с этим примером, вы вернетесь к (М1 ,М2) = (1 ,0), проходя через возможные вводные, и снова получите ошибку. И снова будет применено правило П2, и машина наберется еще немного опыта. На этот раз, когда карту убирают у И1, получается 4.

На этом этапе И1 = 4, И2 = 4, Д = 4. Итак, когда та же ситуация повторится снова, все получится, потому что в игре четыре карты игрока и четыре карты дома. Выход для (М1 ,М2) = (1 ,0) будет 0: «Двух монет НЕТ», а это нам и нужно. Вы также обнаружите, что случай (М1 ,М2) = (1 ,1) тоже дает верный результат. При этом условии конечное уменьшенное значение И1(4) + И2(4) = 8. У дома 4, а 8 >4.

Наша машина научилась действовать правильно только благодаря игре и меняла карты, когда у нее не получалось. Правила игры — обучающий алгоритм.

Поэкспериментируйте с игрой сами. Вы обнаружите, что в какой-то момент придется применить все правила П1–П3 в зависимости от того, какие карты сданы в начале игры. Это поможет машине усвоить правильное поведение. Оно зависит от того, с чего вы начнете, и от порядка, в каком вы будете опускать монеты в щели (разные условия), но в конце концов даст результат. Если по правилам игры требуется взять карт больше, чем осталось у вас на руках, вы прибегаете к старой доброй «долговой расписке». Напишите записку c текстом «–1 карта» или «–2 карты» и продолжайте играть, проверяя, получите ли вы правильный ответ для каждого из условий. В конце останутся значения И1 и И2, которые будут соответствовать либо картам на руках, либо расписке, но игра все равно будет выучена.

В этой игре вы создали самообучающийся модуль для мозга, чтобы вычислять логическую функцию «И». Он учится сообщать, есть ли монеты в щели 1 и в щели 2. Однако мы не программировали логическую функцию «И» — модуль сам научился ее вычислять. Использованный здесь принцип обучения основан на идее нейронной сети.

Нейронная сеть имитирует (моделирует) вычислительные операции мозга на базовом уровне — это абстракция.Миллиарды нервных клеток мозга, называемые нейронами,можно рассматривать как простые устройства обработки данных. Они связаны с другими нейронами с помощью особых отростков аксонови получают сигналы из других частей нейронного контура. Если сигнал, поступивший в часть клетки, называемую синапс,достаточно силен (превышает весовой порог нейрона), то этот нейрон отправляет сигнал к другим, соединенным с ним.