Питер Макоуэн - Вычислительное мышление - Метод решения сложных задач

Чтобы объяснить, как в этом случае происходит обучение, мы используем простую версию самообучающейся машины.Для этого понадобится игровое поле, показанное на рис. 44, и набор карт (не важно, что на них изображено). Сыграв серию раундов этой игры, машина научится правильно определять, есть ли у нее нужное число монет. Игроки кладут (или не кладут) монету на игровое поле, после этого карты перемещают по столу, складывают и сравнивают числа. В итоге машина выдает ответ.

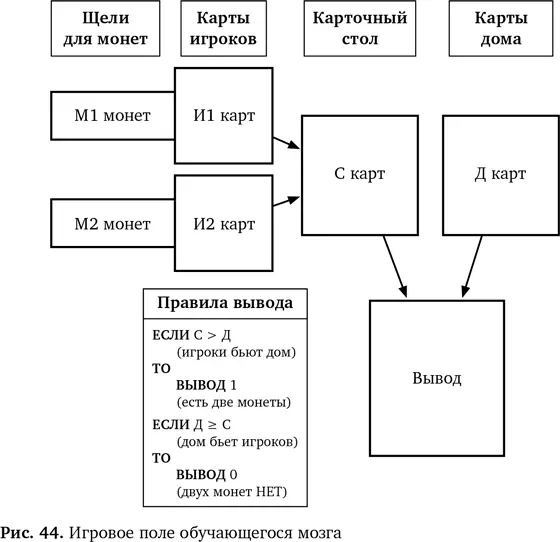
У машины есть две щели, куда каждый из двух игроков помещает монеты, чтобы их посчитали. Карты обоих игроков выкладываются в нужную позицию на поле. Еще есть зона карточного стола, где играют в карты, и зона, куда складывают карты дома. Итоговую карту раунда кладут в последнюю зону — зону выхода. Выбирают из двух итоговых карт, на одной стоит 0, а на второй — 1.

Игра идет слева направо следующим образом. Мы сдаем небольшое произвольное число карт двум игрокам и дому — это, соответственно, И1, И2 и Д. Потом мы играем серию раундов. Каждый игрок должен положить монету в щель, чтобы получить право сыграть раунд. Сделав это, игроки открывают карты — И1 и И2. Эти карты отправляются в зону карточного стола (там они складываются, и мы получаем сумму — С). Сумма играет против дома. Если у игроков больше карт, чем у дома (С >Д), то они выиграли. В этой ситуации выход равен 1. Нам нужно, чтобы в конечном итоге это означало «Есть две монеты». Если выигрывает дом, то выход равен 0, и мы надеемся, что это будет означать «Двух монет НЕТ». В любом случае карты игроков отправляются в начальную точку и начинается следующий раунд.

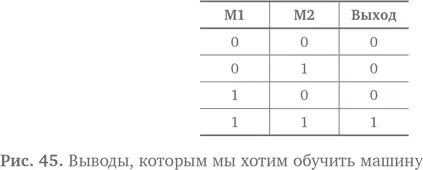
Поскольку мы сдаем произвольное количество карт и оно определяет результат, мозг настольной игры тоже будет действовать произвольно. Нам необходимо, чтобы после многократного повторения игры наш мозг научился менять изначальное случайное число карт на число, которое всегда дает нужный результат. То есть в конце выход должен быть равен 1, только если присутствует две монеты. Результат, которого мы хотим добиться, представлен на рис. 45.

Машина учится это делать в ходе серии раундов, и после каждого раунда мы применяем следующие простые порождающие правила,где М1 обозначает число монет, которое положил игрок 1 (одну монету или ни одной), а М2 — число монет, которое положил игрок 2.

Правило П1:

ЕСЛИсыгранная партия дает правильный выход,

ТОне делайте ничего — не меняйте число карт.

Правило П2:

ЕСЛИсыгранная партия дает на выходе 1, но мы хотели получить 0, чтобы это соответствовало таблице выходов,

ТОзаберите М1 карт у игрока 1 и М2 карт у игрока 2.

Правило П3:

ЕСЛИсыгранная партия дает на выходе 0, но мы хотели получить 1,

ТОдобавьте М1 карт игроку 1 и М2 карт игроку 2.

Эти правила — обучающий алгоритм для нашего мозга. Пора оценитьих, поэтому давайте посмотрим на примеры.

Представим, что сейчас в игре три карты, сданные игроку 1, четыре — игроку 2 и три — дому (И1 = 3 ,И2 = 4 ,Д = 5). В щели 1 есть монета (М1 = 1), а в щели 2 монеты нет (М2 = 0). Мы запишем, что (М1 ,М2) = (1 ,0).

Поскольку в щели 1 есть монета (М1 равно 1), то три карты И1 выкладываются на стол, а карты И2 — не выкладываются, потому что М2 равно 0. Соответственно, на карточном столе у нас три карты (рис. 46).

Можно обобщитьколичество карт (С), которое отправляется на стол. Оно вычисляется с помощью уравнения:

С = ((М1 ×И1) + (М2 ×И2)) .

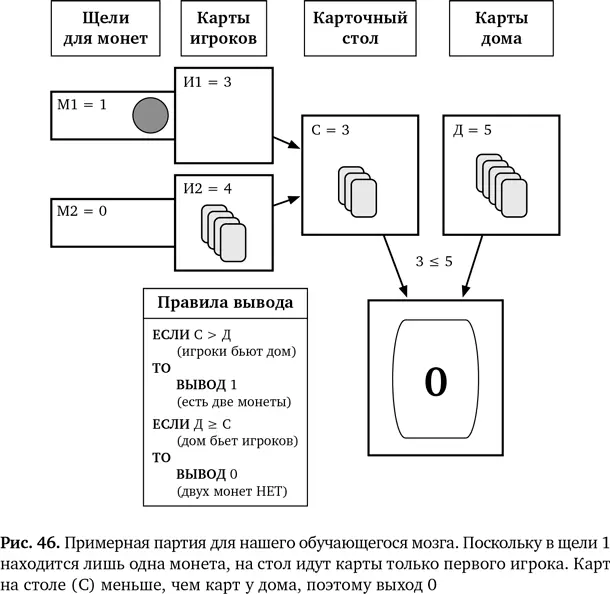
В нашем примере получается (1 ×3 + 0 ×4) = (3 + 0) = 3. Из операции умножения следует, что значения М1 и М2 определяют, будут ли сложены соответствующие суммы. Если М равно 0, то значение И не учитывается в сумме, а если оно равно 1, то значение остается.

Таким образом, сумма С для нашего мозга равна 3, и это меньше, чем Д, равное 5 (3 <5), поэтому карта, помеченная как 0, помещается в зону выхода: «Двух монет НЕТ». Это выход, который мы хотим получить, когда в игре только одна монета. В этом случае мы применяем правило П1 и ничего не делаем.

Теперь попробуем другой вариант. Все карты возвращаются туда, откуда они взяты. Однако на этот раз давайте поместим по монете в обе щели: (М1 ,М2) = (1 ,1). Теперь карты обоих игроков идут на стол, поскольку в обеих щелях есть монеты. И остается семь карт: (1 ×3 + 1 ×4) = 7.