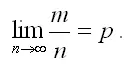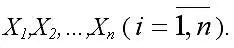Ангелина Яковлева - Ответы на экзаменационные билеты по эконометрике

Однако при использовании теоремы Бернулли необходимо учитывать то, что из неё не следует равенство

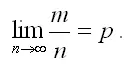
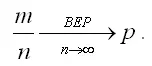
Главным утверждением теоремы является то, что при достаточно большом количестве испытаний относительная частота m/n будет сколь угодно мало отличаться от постоянной вероятности р наступления события в каждом испытании. Другими словами, теорема Бернулли утверждает, что при n› ε относительная частота стремится по вероятности к р . Поэтому теорема Бернулли может быть записана следующим образом:

При проведении статистических исследований, в ходе которых осуществляется сбор данных об исследуемом объекте или процессе, часто сталкиваются с проблемой ошибочности наблюдений. В основе ошибочности наблюдений может лежать как несовершенство методов и инструментов, используемых при проведении статистического исследования, так и заранее непредусмотренные факторы. В связи с этим возникла задача исключения подобных ошибок наблюдения.

Ошибки наблюдения делятся на систематические ошибки и случайные ошибки.

Систематическими ошибкаминаблюдения называются такие ошибки, которые вызваны несовершенством методов и инструментов, применяемых при проведении исследования. Теоретически все систематические ошибки наблюдения могут быть исключены.

Случайными ошибкаминаблюдения называются такие ошибки, которые возникают под воздействием целой совокупности случайных факторов. При этом каждый из этих факторов в отдельности вызывает частичную ошибку, а результатом совместного действия всех случайных факторов является суммарная случайная ошибка, которую уже подлежит оценке.

Допустим, что была проведена серия наблюдений некоторой случайной величины Х . В ходе наблюдений данной случайной величины возникли ошибки, сформированные воздействием множества независимых факторов

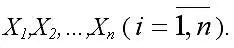
Тогда ошибка а , возникающая в ходе наблюдения случайной величины Х , может быть представлена с помощью выражения:

а=f(X1,X2,…,Xn),

где f – это закономерность образования ошибки.

В связи с тем, что ошибка наблюдений а – величина случайная, то для наиболее точной характеристики данной величины необходимо знать закон распределения её вероятностей. Данная задача решается с помощью теоремы А.М. Ляпунова, также известной под названием центральной предельной теоремы. В качестве одной из математических предпосылок эконометрического моделирования выступает следствие из теоремы Ляпунова.

Следствие теоремы Ляпунова.Если случайная величина Х является суммой очень большого числа попарно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то случайная величина Х подчиняется закону распределения, который близок к нормальному закону распределения вероятностей случайной величины.

Если суммарную ошибку наблюдений рассматривать как сумму очень большого числа попарно независимых частных ошибок, следовательно, то можно сделать вывод, что суммарная ошибка подчиняется закону распределения, который близок к нормальному закону распределения вероятностей.

Главным инструментом эконометрического исследования является модель. Выделяют три основных класса эконометрических моделей:

1) модель временных рядов;

2) модели регрессии с одним уравнением;

3) системы одновременных уравнений.

Моделью временных рядовназывается зависимость результативной переменной от переменной времени или переменных, относящихся к другим моментам времени.

К моделям временных рядов, характеризующих зависимость результативной переменной от времени, относятся:

а) модель зависимости результативной переменной от трендовой компоненты или модель тренда;

б) модель зависимости результативной переменной от сезонной компоненты или модель сезонности;

в) модель зависимости результативной переменной от трендовой и сезонной компонент или модель тренда и сезонности.

К моделям временных рядов, характеризующих зависимость результативной переменной от переменных, датированных другими моментами времени, относятся: