Валентин Арьков - Бизнес-аналитика. Сводные таблицы. Часть 2. Учебное пособие

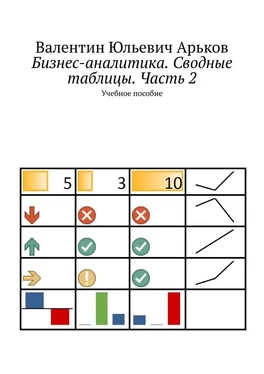
Кстати, это пример ситуации, когда ДАННЫЕ и ИНФОРМАЦИЯ – не одно и то же. Много данных в виде цифр – это не обязательно много полезной информации. Это просто цифры. А информация должна быть ПОЛЕЗНОЙ для дела.

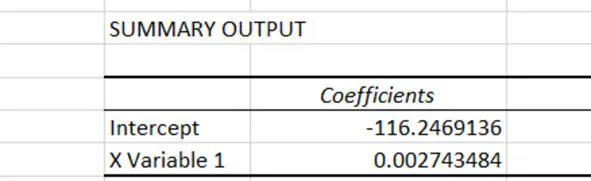
Рис. 4.18. Результаты регрессионного анализа

Задание. Запишите уравнение тренда с точностью до пяти значащих цифр.

Сезонные колебания – это изменения с периодом в один год. То есть двенадцать месяцев, или примерно 365 дней. Сезон – это времена года и всё, что с ними связано.

Причина сезонных колебаний цен – это изменение количества товаров, которое предлагается на рынке. В экономике это называется ПРЕДЛОЖЕНИЕ. Понятно, что сразу после сбора урожая сельскохозяйственной продукции много, и цены обычно снижаются. А вот когда запасы подходят к концу, цена может вырасти. Эта картина повторяется каждый год.

Мы будем моделировать сезонные колебания цен в диапазоне плюс-минус 10% от среднего значения цены. Пусть все цены достигают минимального значения в октябре каждого года. И пусть они меняются по синусоиде.

Пусть минимум будет 1 октября 2018 года. Находим порядковый номер этого дня, как мы уже проделали в предыдущем разделе (рис. 4.19). Получаем число

t (min) = 43104.

Это не наименьшее время.

Это день, когда цены минимальные.

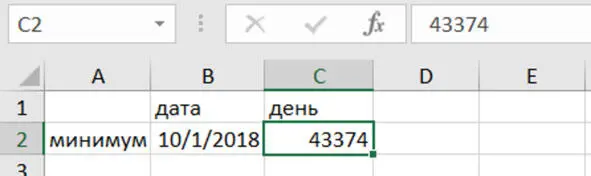
Рис. 4.19. Дата минимальных цен

Определим начало периода синусоидальных колебаний (рис. 4.20). Это будет номер дня 1 октября 2018 года минус 9 месяцев, то есть минус 9*30 = 270 дней:

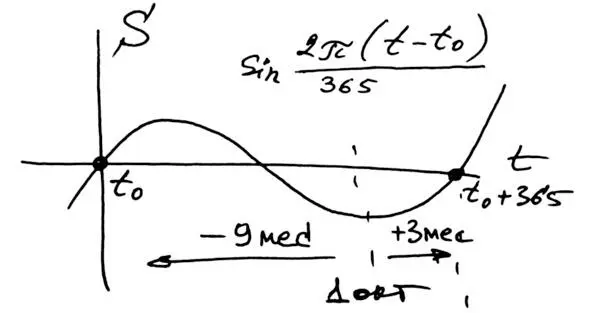
Рис. 4.20. Начало периода колебаний

Таким образом, получаем начало периода колебаний (рис. 4.21).

t 0= 43374 – 270 = 43104.

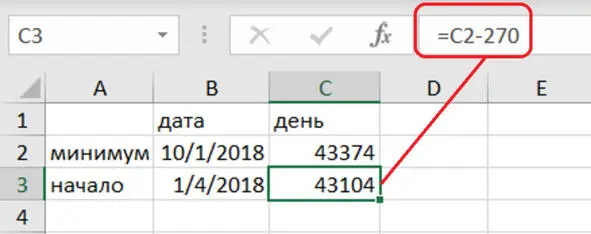
Рис. 4.21. Начало периода колебаний

Мы собираемся моделировать колебания в пределах плюс-минус 10% средней цены. В этом случае придётся использовать мультипликативную модель [3]. Так что в уравнении сезонных колебаний это будут колебания вокруг единицы с амплитудой 0,1 (рис. 4.22).

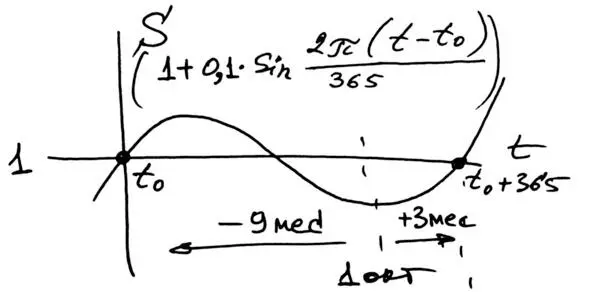
Рис. 4.22. Мультипликативная модель

Конечно, это очень упрощённая модель. Форма колебаний не похожа на синусоиду. А время сбора урожая различается для моркови и для орехов.

В наших упражнениях самое главное – почувствовать саму идею. А если будет желание, можно сделать более реалистичное описание.

Задание. Запишите формулу сезонных колебаний цен с конкретными числовыми параметрами.

Наша модель будет дополнительно учитывать «рациональное» поведение покупателей. Будем считать, что клиенты стремятся покупать большее количество, когда цены падают. И стараются экономить при повышении цен, то есть покупать меньшее количество товара.

В нашей модели количество покупаемого товара, то есть СПРОС, будет переживать сезонные колебания. Колебания будут в противоположной фазе в сравнении с колебаниями цен. То есть 1 октября будет максимум покупок. Соответственно, начало периода колебаний – это 1 октября минус три месяца:

t 0= 43374 – 3*30 = 43374 – 90 = 43284.

Это начало июля. К началу октября покупки растут. К январю цены выросли, а закупки упали. И так повторяется каждый год.

Задание. Запишите уравнение сезонных колебаний спроса с конкретными значениями коэффициентов.

Мы заложили в нашу модель взаимосвязь между уровнем цен и спросом, то есть количеством купленного товара. Это зависимость в среднем – на фоне случайного разброса, отклонений. Наличие такой зависимости называется КОРРЕЛЯЦИЯ (рис. 4.23). Слово «корреляция» происходит от латинского correlatio – «соотношение, взаимосвязь», где co – — «со-, взаимо-, вместе» и relatio – «отнесение, связь». Если в среднем значение увеличивается, это прямая корреляция, если уменьшается – то обратная.

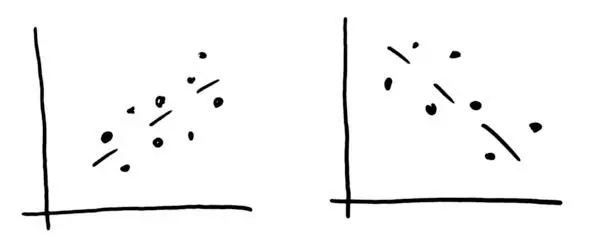
Рис. 4.23. Прямая и обратная корреляция