Евгений Сидоркин - КНИГА-ТРЕНАЖЕР - «Базовая подготовка к ЕГЭ по информатике в компьютерной форме». Авторский курс

Рисунок №6

Вы еще не устали от логики)?

Последняя функция эквиваленция. Обозначается как на рисунке №6.

Рисунок №6

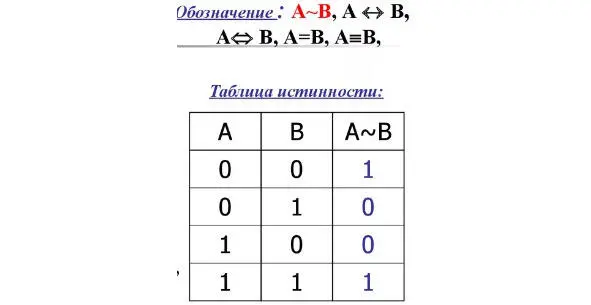
Функция истинна A <-> B=1 только в двух случаях: либо когда обе логических переменных А и B истинны, или когда А и B – ложны.

В каком же приоритете выполняются данные операции, спросите Вы? Да все очень просто: сначала отрицание, затем конъюнкция (умножение), потом дизъюнкция (сложение), далее импликация и эквиваленция.

Рисунок №7

В ЕГЭ представлено две задачи на знания алгебры логики. Это задачи №2 и №15. Рассмотрим основные типы этих задач ниже.

Пример 2.1

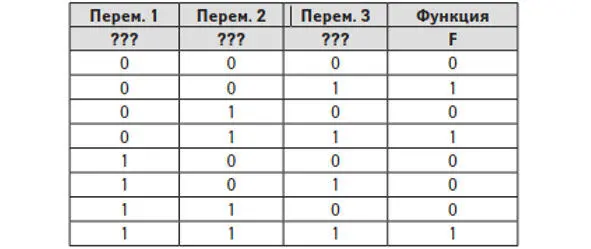
Логическая функция F задается выражением (x ⟶ y) ∧ (x ∨ ¬z) ∧ (x ≣ ¬w). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных w, x, y, z.

Решение:

Первый способ – это написание программы на языке программирования Python. Код представлен ниже.

После запуска программы мы можем заметить строку, содержащую 0 0 0 1. Если сравнить эту строку со строками из таблицы (что в условии), то в данной таблице мы не найдем строку с тремя нулями, поэтому строку 0 0 0 1 можем смело исключить из решения. Рассмотрим оставшиеся три строки, которые необходимо сопоставить с таблицей, что в условии. Второй столбец с тремя единицами соответствует второму столбцу из таблицы, значит, второй столбец – Y. В первую ячейку третьего столбца однозначно можно поставить только ноль, и тогда образуется первая строка 1 1 1 0. Т.к. в последней строчке из рисунка №7 стоит такая же строка 1 1 1 0, что в условиях таблицы, то третий столбец – однозначно W. На рисунке №7 в первой и третьей ячейке третьей строки стоят нули, которые мы можем перенести в таблицу из условия на соответствующие места и однозначно определить, что Z – это первый столбец, а Z – третий.

Второй способ решения этой же задачи состоит в том, что мы составляем таблицу истинности без помощи компьютера. Заполняем первую строку, если w=0, то x=1, а y=1, а z – или ноль, или один. Итого получим почти две одинаковые строчки, за исключением значения z. 1 1 0 0 и 1 1 1 0. Теперь предположим, что W=1, тогда x=0. Т.к. в условии есть столбец с тремя единицами, то необходимо в ручном решении тоже получить такой столбец, поэтому y=1, а z=0. Ответ: ZYWX.

Пример 2.2

Логическая функция F задается выражением (¬z) ∧ x ∨ x ∧ y. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

Решение:

Расставим скобки, выражение (¬z) ∧ x ∨ x ∧ y является дизъюнкцией двух конъюнкций: ((¬z) ∧ x) ∨ (x ∧ y). В обеих конъюнкциях присутствует x. То есть при x = 0 все выражение равно нулю. Только в третьем столбце напротив нулей стоят значения функции F=0, поэтому третий столбец – это x. Также можно заметить, что выражение ((¬z) ∧ x) ∨ (x ∧ y) =1, если x =1 и выполняется хотя бы одно из условий: y = 1 или z = 0. Из четвертой строки следует, что Перем.1 = z, а Перем.2 = y.

Ответ : zyx.

Пример 2.3

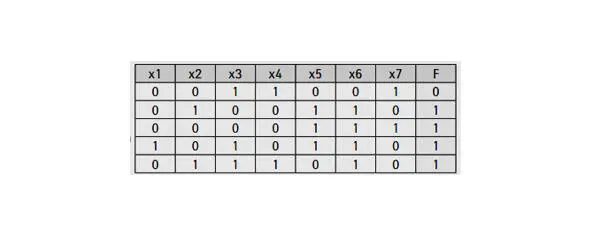
Дан фрагмент таблицы истинности для выражения F. Укажите максимально возможное число различных строк полной таблицы истинности этого выражения, в которых значения x4 не совпадает с F.

Решение:

Таблица истинности выражения с семью переменными (x1…x7) содержит 2 7=128 строк. В приведенном фрагменте таблицы x4 не совпадает с F в 4-х строках, а совпадает только в последней нижней строке. Во всех остальных может не совпадать. Тогда максимально возможное количество строк, где значения x4 и F не совпадают, будет 128—1=127.