В. И. Григорьев.
Инвариантность (в системах автоматического регулирования)
Инвариа'нтность,в системах автоматического регулирования, независимость какой-либо системы от приложенных к ней внешних воздействий. Независимость одной из регулируемый координат системы от всех внешних воздействии или независимость всех координат от одного какого-либо воздействия называется полиинвариантностью. Часто условия И. не могут быть выполнены точно; в этом случае говорят об И. с точностью до некоторой наперёд заданной величины. Для реализуемости условий И. необходимо наличие в системе по меньшей мере двух каналов распространения воздействия между точкой приложения внешнего воздействия и координатой, И. которой должна быть обеспечена (принцип двухканальности Б. Н. Петрова ). Идеи И. применяют в системах автоматического управления летательными аппаратами, судами, для управления химическими процессами при построении следящих систем и особенно комбинированных систем, в которых одновременно используются принципы регулирования по отклонению и по возмущению.
Лит.: Кухтенко А. И., Проблема инвариантности в автоматике, К. ,1963; Петров Б. Н., Рутковский В. Ю., Двухкратная инвариантность систем автоматического управления, «Докл. АН СССР», 1965, т. 161, № 4.
В. Ю. Рутковский.
Инвариа'нты(от лат. invarians, родительный падеж invariantis — неизменяющийся), числа, алгебраические выражения и т. п., связанные с каким-либо математическим объектом и остающиеся неизменными при определенных преобразованиях этого объекта или системы отсчёта, в которой описывается объект. Чтобы охарактеризовать какую-либо геометрическую фигуру и её положение с помощью чисел, обычно приходится вводить некоторую вспомогательную систему отсчёта или систему координат. Полученные в такой системе числа x 1, x 2,..., x nхарактеризуют не только изучаемую геометрическую фигуру, но и её отношение к системе отсчёта, и при изменении этой системы фигуре будут отвечать другие числа x ¢ 1, х ¢ 2,..., х ¢ n. Поэтому если значение какого-либо выражения f ( x 1, x 2,..., x n) характерно для фигуры самой по себе, то оно не должно зависеть от системы отсчёта, т. е. должно выполняться соотношение
f ( x 1, x 2,..., x n) = f ( x ¢ 1, x ¢ 2,..., x ¢ n). (1)
Все выражения, удовлетворяющие соотношению (1), называются инвариантами. Например, положение отрезка M 1 M 2на плоскости определяется в прямоугольной системе координат двумя парами чисел x 1, y 1и x 2, y 2— координатами его концов M 1и M 2. При преобразовании координатной системы (путём смещения её начала и поворота осей) точки M 1и M 2получают другие координаты x ¢ 1, у ¢ 1и x ¢ 2, у ¢ 2, однако ( x 1— x 2) 2+ ( y 1— y 2) 2= ( x ¢ 1— x ¢ 2) 2+ ( y ¢ 1— у ¢ 2) 2. Поэтому выражение ( x 1— x 2) 2+ ( y 1— — y 2) 2является И. преобразования прямоугольных координат. Геометрический смысл этого И. ясен: это квадрат длины отрезка M 1 M 2.
Кривая 2-го порядка в прямоугольной системе координат задаётся уравнением 2-й степени
ax 2+ 2 bxy + cy 2 + 2dx + 2ey + f = 0, (2)
коэффициенты которого можно рассматривать как числа, определяющие кривую. При преобразовании прямоугольных координат эти коэффициенты изменяются, но выражение 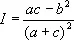 сохраняет свое значение и, следовательно, служит И. кривой (2). При рассмотрении кривых и поверхностей высших порядков возникает аналогичная более общая задача.
сохраняет свое значение и, следовательно, служит И. кривой (2). При рассмотрении кривых и поверхностей высших порядков возникает аналогичная более общая задача.
Понятие И. употреблялось ещё немецким математиком О. Гессе (1844), но систематическое развитие теория И. получила у английского математика Дж. Сильвестра (1851—52), предложившего и термин «И.». В течение 2-й половины 19 в. теория И. была одной из наиболее разрабатываемых математических теорий. В процессе развития этой классической теории И. главные усилия исследователей стали постепенно сосредоточиваться вокруг решения нескольких «основных» проблем, наиболее известная из которых формулировалась следующим образом. Рассматриваются И. системы форм, являющиеся целыми рациональными функциями от коэффициентов этих форм. Требуется доказать, что для И. каждой конечной системы форм существует конечный базис, т. е. конечная система целых рациональных И., через которые каждый другой целый рациональный И. выражается в виде целой рациональной функции. Это доказательство для проективных И. было дано в конце 19 в. немецким математиком Д. Гильбертом.
Читать дальше

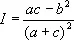 сохраняет свое значение и, следовательно, служит И. кривой (2). При рассмотрении кривых и поверхностей высших порядков возникает аналогичная более общая задача.
сохраняет свое значение и, следовательно, служит И. кривой (2). При рассмотрении кривых и поверхностей высших порядков возникает аналогичная более общая задача.