поэтому в этом случае пишут
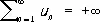 .
.
Для Р. с неотрицательными членами имеется ряд признаков сходимости.
Интегральный признак сходимости: если функция f ( х ) определена при всех х ³ 1, неотрицательна и убывает, то Р.
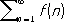 (7)
(7)
сходится тогда и только тогда, когда сходится интеграл
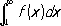 .
.
С помощью этого признака легко устанавливается, что Р.
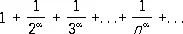 (8)
(8)
сходится при a > 1 и расходится при a £ 1.
Признак сравнения: если для двух Р. (1) и (6) с неотрицательными членами существует такая постоянная с > 0, что 0 £ u n £ c u n , то из сходимости Р. (6) следует сходимость Р. (1), а из расходимости Р. (1) — расходимость Р. (6). Обычно для сравнения берётся Р. (8), а в заданном Р. выделяется главная часть вида А/n a . Таким методом сразу получается, что Р. с n -м членом
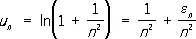 ,
,
где
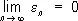
сходится, поскольку сходится Р.
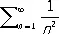 .
.
Как следствие признака сравнения получается следующее правило: если
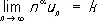
то при a > 1 и 0 £ k < + ¥ Р. сходится, а при a £ 1 и 0 < k £ + ¥ Р. расходится. Так, например, Р. с n -м членом u n = sin (1/ n 2) сходится, ибо
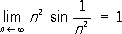 (a = 2)
(a = 2)
a Р. с u n = tg (p/ n ) расходится, здесь
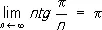 (a = 1)
(a = 1)
Часто оказываются полезными два следствия признака сравнения. Признак Д'Аламбера: если существует 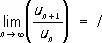 ( u n> 0), то при l < 1 P. (1) сходится, а при l > 1 — расходится; и признак Коши: если существует
( u n> 0), то при l < 1 P. (1) сходится, а при l > 1 — расходится; и признак Коши: если существует 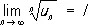 ( u n³ 0), то при l < 1 P. (1) сходится, а при l > 1 P. расходится. При I = 1 как в случае признака Д'Аламбера, так и в случае признака Коши существуют и сходящиеся и расходящиеся Р.
( u n³ 0), то при l < 1 P. (1) сходится, а при l > 1 P. расходится. При I = 1 как в случае признака Д'Аламбера, так и в случае признака Коши существуют и сходящиеся и расходящиеся Р.
Важный класс Р. составляют абсолютно сходящиеся ряды: Р. (1) называется абсолютно сходящимся, если сходится Р.
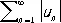 .
.
Если Р. абсолютно сходится, то он и просто сходится. Р.
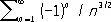
абсолютно сходится, а Р.
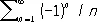
сходится, но не абсолютно. Сумма абсолютно сходящихся Р. и произведение абсолютно сходящегося Р. на число являются также абсолютно сходящимися Р. На абсолютно сходящиеся Р. наиболее полно переносятся свойства конечных сумм. Пусть
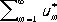 (9)
(9)
— P., составленный из тех же членов, что и Р. (1), но взятых, вообще говоря, в другом порядке. Если Р. (1) сходится абсолютно, то Р. (9) также сходится и имеет ту же сумму, что и Р. (1). Если Р. (1) и Р. (6) абсолютно сходятся, то Р., полученный из всевозможных попарных произведений u m u n членов этих Р., расположенных в произвольном порядке, также абсолютно сходится, причём если сумма этого Р. равна s , а суммы Р. (1) и (6) равны соответственно s 1и s 2, то s = s 1s 2, т. е. абсолютно сходящиеся Р. можно почленно перемножать, не заботясь о порядке членов. Признаки сходимости для Р. с неотрицательными членами применимы для установления абсолютной сходимости рядов.
Для Р., не абсолютно сходящихся (такие Р. называют также условно сходящимися), утверждение о независимости их суммы от порядка слагаемых неверно. Справедлива теорема Римана: посредством надлежащего изменения порядка членов данного не абсолютно сходящегося Р. можно получить Р., имеющий наперёд заданную сумму, или расходящийся Р. Примером условно сходящегося Р. может служить Р.
Читать дальше

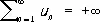 .
.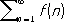 (7)
(7)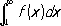 .
.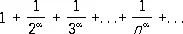 (8)
(8)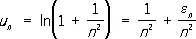 ,
,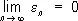
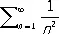 .
.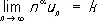
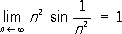 (a = 2)
(a = 2)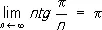 (a = 1)
(a = 1)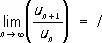 ( u n> 0), то при l < 1 P. (1) сходится, а при l > 1 — расходится; и признак Коши: если существует
( u n> 0), то при l < 1 P. (1) сходится, а при l > 1 — расходится; и признак Коши: если существует 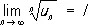 ( u n³ 0), то при l < 1 P. (1) сходится, а при l > 1 P. расходится. При I = 1 как в случае признака Д'Аламбера, так и в случае признака Коши существуют и сходящиеся и расходящиеся Р.
( u n³ 0), то при l < 1 P. (1) сходится, а при l > 1 P. расходится. При I = 1 как в случае признака Д'Аламбера, так и в случае признака Коши существуют и сходящиеся и расходящиеся Р.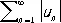 .
.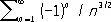
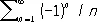
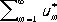 (9)
(9)