Одни и те же величины могут выражаться через суммы различных рядов. Так, для числа p, кроме Р. (3), имеются и другие Р., например
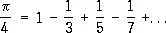 ,
,
однако он сходится значительно «медленнее» Р. (3), и потому его невыгодно использовать для приближённого вычисления числа p . Существуют методы преобразования Р., иногда улучшающие скорость сходимости Р.
На бесконечные суммы не переносятся все свойства конечных сумм. Например, если взять Р.
1 - 1 + 1 - 1 +... (5)
и сгруппировать подряд его члены по два, то получим (1—1) + (1—1) +... = 0; при другом же способе группировки 1 — (1 — 1) — (1 — 1) —... = 1. Поэтому следует дать чёткое определение того, что называется бесконечной суммой, и, определив это понятие, проверить, справедливы ли для таких сумм закономерности, установленные для конечных сумм. Доказывается, что для бесконечного числа слагаемых при определённых условиях сохраняются законы коммутативности и ассоциативности сложения, дистрибутивности умножения относительно сложения, правила почленного дифференцирования и интегрирования и т. п.
Числовые ряды.Формально Р. (1) можно определить как пару числовых (действительных или комплексных) последовательностей { u n } и { S n} таких, что S n = u 1+... + u n, n = 1, 2,... Первая последовательность называется последовательностью членов Р., а вторая — последовательностью его частичных сумм [точнее S nназывается частичной суммой n- го порядка Р. (1)]. Р. (1) называется сходящимся, если сходится последовательность его частичных сумм { S n} . В этом случае предел
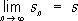
называется суммой Р. и пишется
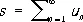
Т. о., обозначение (1) применяется как для самого Р., так и для его суммы (если он сходится). Если последовательность частичных сумм не имеет предела, то Р. называется расходящимся. Примером сходящегося Р. является Р. (2), расходящегося — Р. (5). Каждый Р. однозначно определяет последовательность его частичных сумм, и обратно: для любой последовательности { s n} имеется и притом единственный Р., для которого она является последовательностью его частичных сумм, причём члены u nэтого Р. определяются по формулам u 1 = s 1,..., u n+1 = s n + 1 — s n ,..., n = 1, 2,... В силу этого изучение Р. эквивалентно изучению последовательностей.
Р. 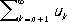 называется остатком порядка n Р. (1). Если Р. сходится, то каждый его остаток сходится, а если какой-либо остаток Р. сходится, то и сам Р. также сходится. Если остаток порядка n Р. (1) сходится и его сумма равна r n , то s = s n + r п.
называется остатком порядка n Р. (1). Если Р. сходится, то каждый его остаток сходится, а если какой-либо остаток Р. сходится, то и сам Р. также сходится. Если остаток порядка n Р. (1) сходится и его сумма равна r n , то s = s n + r п.
Если Р. (1) и Р.
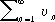
сходятся, то сходится и Р.
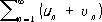 ,
,
называемый суммой рядов (1) и (6), причем его сумма равна сумме данных Р. Если Р.(1) сходится и l — комплексное число, то Р.
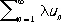 ,
,
называемый произведением Р. на число l, также сходится и
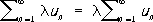 .
.
Условие сходимости Р., не использующее понятия его суммы (в случаях, когда, например, сумма Р. неизвестна), даёт критерий Коши: для того чтобы Р. (1) сходился, необходимо и достаточно, чтобы для любого e > 0 существовал такой номер n e, что при любом n ³ n eи любом целом р ³ 0 выполнялось неравенство
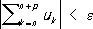 .
.
Отсюда следует, что если Р. (1) сходится, то
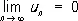
Обратное неверно: n -й член так называемого гармонического ряда
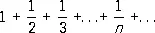
стремится к нулю, однако этот Р. расходится.
Большую роль в теории Р. играют Р. с неотрицательными членами. Для того чтобы такой Р. сходился, необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена сверху. Если же он расходится, то
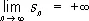 ,
,
Читать дальше

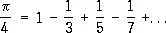 ,
,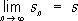
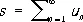
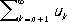 называется остатком порядка n Р. (1). Если Р. сходится, то каждый его остаток сходится, а если какой-либо остаток Р. сходится, то и сам Р. также сходится. Если остаток порядка n Р. (1) сходится и его сумма равна r n , то s = s n + r п.
называется остатком порядка n Р. (1). Если Р. сходится, то каждый его остаток сходится, а если какой-либо остаток Р. сходится, то и сам Р. также сходится. Если остаток порядка n Р. (1) сходится и его сумма равна r n , то s = s n + r п.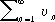
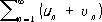 ,
,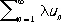 ,
,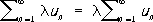 .
.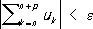 .
.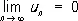
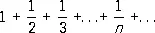
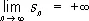 ,
,