Джонс Морган - Решение проблем по методикам спецслужб. 14 мощных инструментов

Ответ: «Два доллара». Записываем эту цифру в колонке «Полезность» рядом с вариантом последствий «красная» (рис. 14.4). Затем задаем тот же вопрос в отношении второго сценария (ставка на красную конфету, но вытягиваем желтую): «Если я сделаю ставку на красную конфету, но вытяну желтую, какова полезность этого события?» Ответ: «Ноль долларов». На этот же вопрос нужно ответить для оставшихся семи сценариев и записать результат.

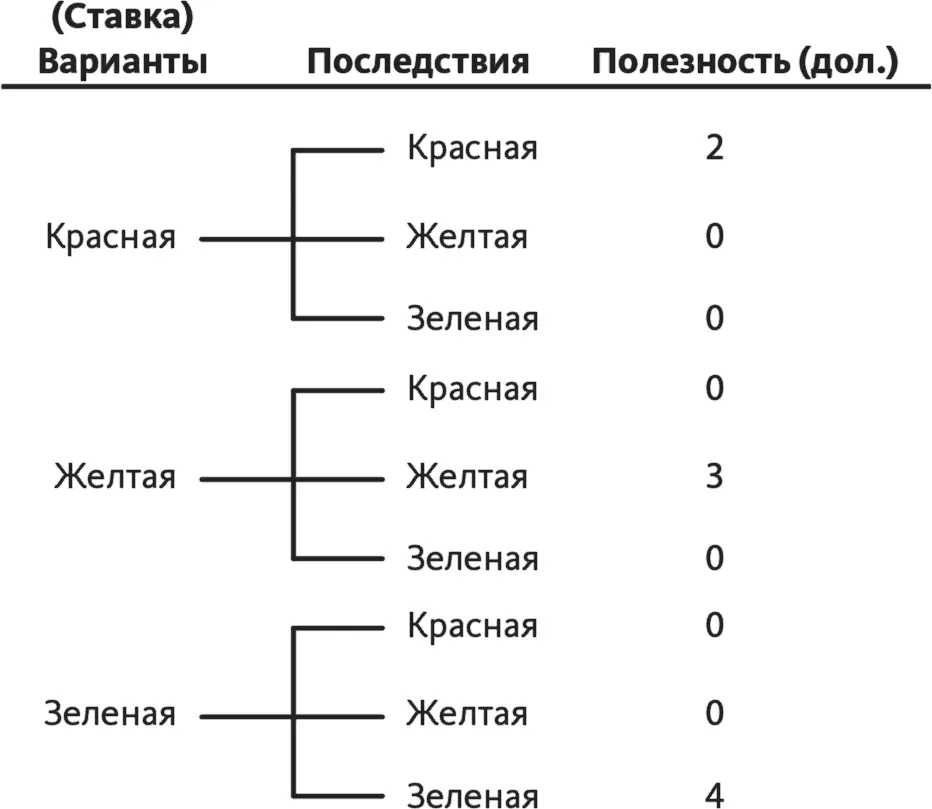
Рис. 14.4.Точка зрения: прибыль того, кто делает ставку

В нашей задаче последствия определены в долларах, поэтому оценить полезность каждого из них несложно, ведь мы привыкли рассматривать ценность именно в денежном выражении. Чуть позже мы обсудим задачи, в которых полезность не выражается в деньгах.

Какой из трех вариантов дает нам максимальные преимущества, то есть максимальную полезность? Кажется очевидным, что это зеленая конфета, приносящая четыре доллара. Но действительно ли выгоднее всего выбирать зеленую конфету? Подумайте сами: на скачках ставят ли все на ту лошадь, где возврат на ставку может быть максимальным? Все ли ставят на возможность выигрыша 100 к 1? Нет, конечно! Все делают ставки с учетом вероятности выигрыша. Вероятности! Кажется, мы снова к ней вернулись? Зеленая конфета несомненно обеспечивает наивысшую полезность, то есть максимальный приз, но, чтобы решение наше было разумным и обоснованным, нужно учесть и вероятность вытащить именно зеленую конфету.

Приз (то есть полезность) – это то, что мы хотим получить: мы хотим получить четыре доллара. Но наши шансы получить эти четыре доллара определяются вероятностью вытащить зеленую конфету. Повторю: полезность определяет наши желания; вероятность – наш возможный выигрыш. То есть полезность – некий идеальный мир, а вероятность – реальный мир. Запомните это крепко-накрепко. Это очень важная мысль… одна из важнейших в этой книге. Было бы прекрасно, если бы все мы, включая и меня, всегда помнили об этом правиле и применяли его, принимая важные решения, влияющие и на нашу жизнь, и на жизнь многих других. Но часто мы забываем о вероятности, ослепленные желанием получить максимальный выигрыш.

Итак, в ходе анализа задачи про конфеты нужно учесть и вероятность того, что нам удастся вытянуть красную, желтую или зеленую конфету. Для этого мы на пятом шаге задаем себе вопрос для оценки вероятности: «Если мы выбираем этот вариант, какова вероятность наступления этих последствий?» Применительно к первому сочетанию «вариант – последствия» на нашей схеме (ставка на красную, вытягиваем красную) вопрос будет звучать так: «Если я сделаю ставку на то, что вытащу красную конфету, какова вероятность того, что я в самом деле вытащу красную?» В банке 90 конфет: 45 красных, 36 желтых и 9 зеленых. Поэтому вероятность вытащить красную конфету составляет 0,5, желтую – 0,4, зеленую – 0,1. Записываем эти значения на дерево (рис. 14.5). Заметим, что сумма вероятностей всех возможных последствий каждого из вариантов должна равняться единице.

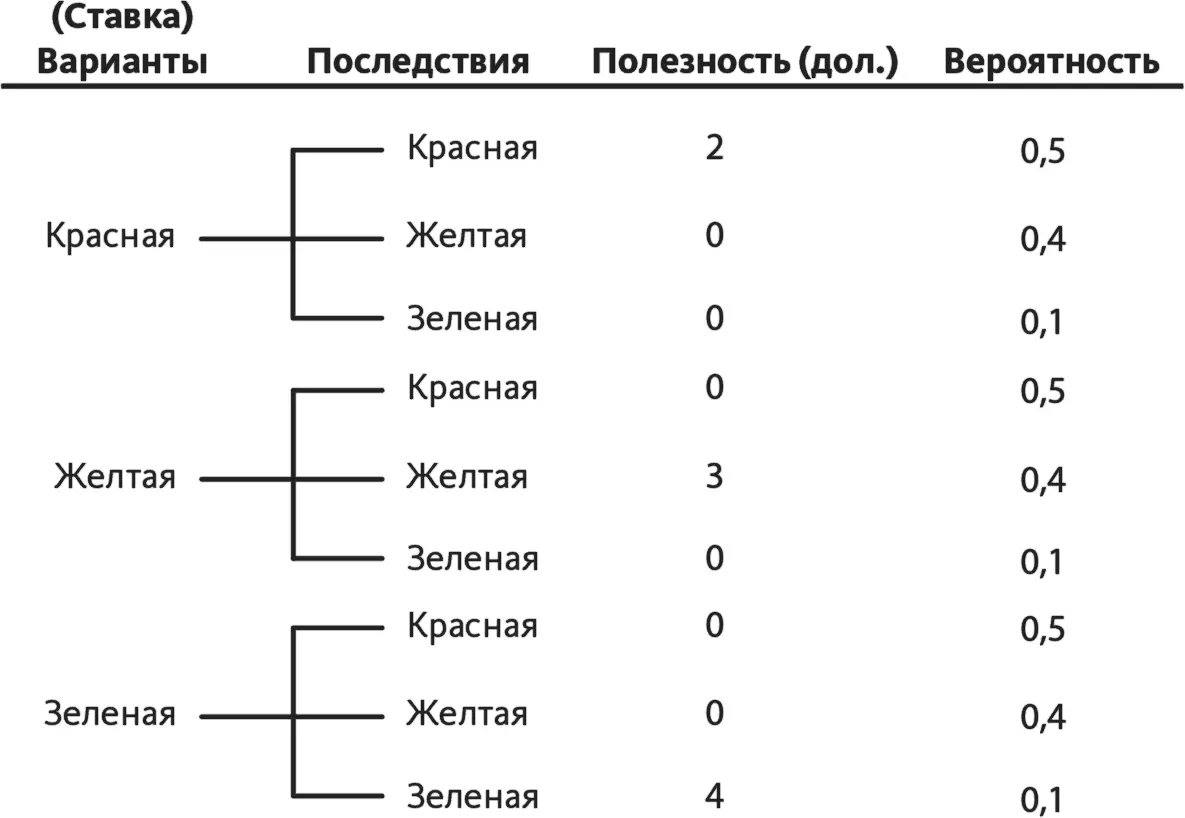
Рис. 14.5.Точка зрения: прибыль того, кто делает ставку

Мы определили полезность каждого из трех вариантов (два, три и четыре доллара), а также вероятность каждого из них (0,5, 0,4 и 0,1). Как нам использовать эти цифры для принятия окончательного решения о том, на что выгоднее всего делать ставку? В этом нам поможет любопытная концепция под названием ожидаемая полезность.

Ожидаемая полезность – это произведение полезности и вероятности последствий. Почему их нужно перемножать? Потому что полезность последствий обусловлена вероятностью их наступления. Мы получаем ожидаемую полезность только при условии, что последствия наступают, то есть мы получим четыре доллара, только если вытащим зеленую конфету. (Полезность – это то, чего мы хотим; вероятность определяет, что именно мы получим.) Эта взаимосвязь выражается в произведении полезности ожидаемых последствий на вероятность их наступления. По этой же логике мы перемножили показатели вероятностей взаимосвязанных событий. Перемножение мы делаем на шестом шаге, результат записываем в колонку «Ожидаемая полезность» (рис. 14.6).

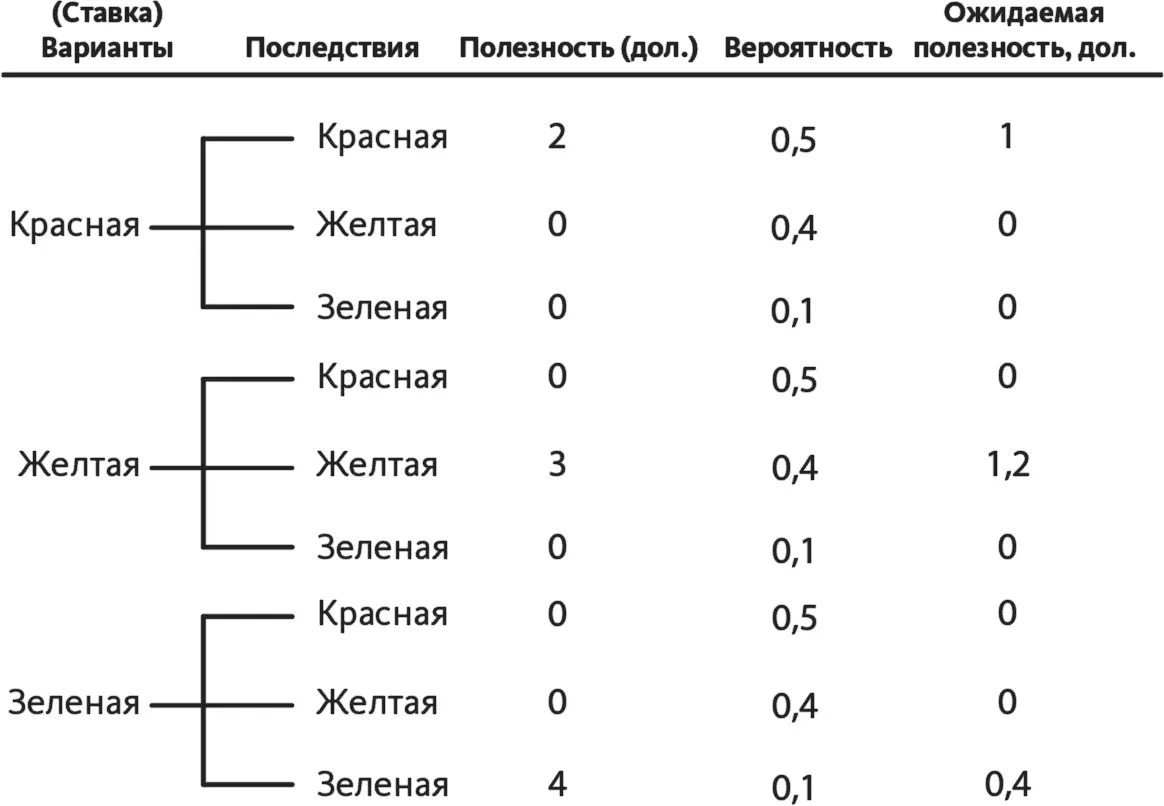
Рис. 14.6.Точка зрения: прибыль того, кто делает ставку