Вильгельм Оствальд - Искусство цвета. Цветоведение - теория цветового пространства

Ниже нами будет изложен и другой путь установления связи между нашим цветовым кругом и спектром, путь, свободный от имеющихся здесь недостатков (см. учение о цветовом полукруге).

Результаты этих измерений, над которыми, вместе со мной работали и другие исследователи, наглядным образом представлены на рис. 6. Внутренний круг разбит на сто равных делений рационально составленного цветового круга. На наружном нанесены длины волн в миллионных долях миллиметра, сответствующие обозначенным внутри круга цветовым тонам.

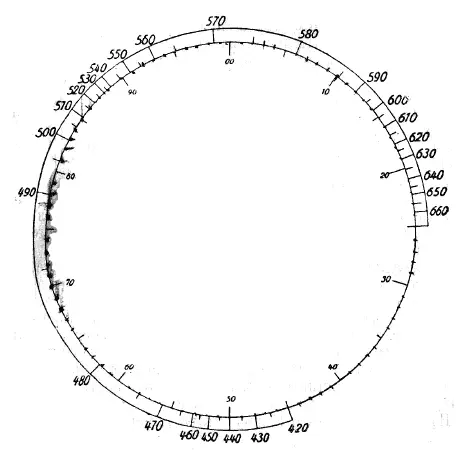
Рис. 6

Если начнем с 1-го желтого, с обозначением 00, то соответствующая ему длина волны будет 572. До начала оранжевого у 13 длина волн очень; удалена друг от друга. Другими словами: в узкую область между 572 и 592 втиснуты 13 цветовых тонов, начиная с самого светлого серно-желтого и кончая оранжевым. В действительности, с помощью спектроскопа, мы можем видеть, что желтые цвета занимают в спектре особенно узкое пространство. Наоборот, оранжевым цветам (до киновари 25) соответствует большая область разной длины волн, а именно – от 592 до 670, – конца видимого спектра. Соответственно этому мы и видим в спектре широкую полосу желто-красного и красного.

Дальше следуют цвета пурпурные, которые в спектре отсутствуют. У 45, синевато-фиолетового, начинаются цвета спектра с самыми короткими волнами, которые проявляют опять большую густоту различных длин волн на протяжении узкого участка между крайним фиолетовым и первым ультрамариново-синим, сообразно большому протяжению фиолетового и ультрамаринового цветов в спектре. На долю ледяного синего и морского зеленого приходится всего лишь немного различных длин волн (от 475 до 500), поэтому в спектре эти цвета занимают лишь узкую полосу. Зато лиственному зеленому и части морского зеленого соответствует опять большое количество волн различной длины. Пределы их – от 500 до 572, где последняя, уже достаточно желтая часть, непосредственно переходит в начало желтого цвета.

Все эти многообразия цветов более ярко выступают в диффракционном спектре, чем в сжатом с красного конца призматическом спектре. Если диффракционный спектр не очень растянут, то в нем видны бывают только три области: глубоко-красная, средне-зеленая и ультрамариново-синяя. Промежуточные же области – желтая и ледяной синий цвет – почти невидимы.

О простой зависимости между длиной волны (или числом колебаний) и цветом не может, следовательно, быть и речи. Безусловно, здесь есть какая-то закономерная зависимость, но настолько сложная, что всякая попытка обосновать, например, гармонию цветов на числе колебаний должна быть заранее обречена на неудачу.

Эти соотношения отчасти были отмечены уже раньше. Так, еще Гельмгольц указывал на особую растянутость в спектре областей красного и ультрамариново-синего цветов. Так как до сих пор отсутствует точное, рациональное и психологически обоснованное расположение цветов в цветовом круге, то эти соотношения еще не нашли себе определенного выражения. Хотя у Геринга расположение основных точек согласно его теории четырех цветов в общем и целом правильное, но он не обладал методами для точного дальнейшего подразделения цветового круга, и потому не сумел связать его с соответствующими длинами волн.

Здесь будет уместно вернуться к работе Кёнига и Дитеричи, о которой было упомянуто выше. Если психологический круг цветовых тонов и круг, изображающий длины волн, располагаются таким причудливым образом, то и разностный порог различия цветовых тонов бывает то больше, то меньше. Разностная чувствительность должна быть больше там, где небольшое число различных длин дает большое число цветовых тонов, и меньше там, где тон цвета очень мало меняется с изменением длины волн. Величины порога чувствительности расположены, конечно, в обратном порядке. К таким выводам пришли названные исследователи. На рис. 7 кривые I и II доказывают изменение величины порога чувствительности (вероятная ошибка установки, выраженная в длинах волн) в зависимости от длины волны: разные кривые принадлежат различным исследователям и относятся к разным силам света. Кривая III изображает содержание рис. 6 или расположение длины волн в рациональном круге цветовых тонов. Ординатами здесь служат различия в длине волн двух соседних ступеней сточленного круга. Эти кривые передают реальные отношения и показывают нам, что ординаты растут и падают в зависимости от изменения величины порога чувствительности. Сходство кривых бросается в глаза и между кривыми III, с одной стороны и I , оно даже больше, чем между I и II .