Вильгельм Оствальд - Искусство цвета. Цветоведение - теория цветового пространства

Особенно ясным и часто применяемым способом для нахождения хорошо понятных гармоний является расщепление. Исходят, например, из какой-нибудь простой двойной гармонии (дополнительные цвета, неполная тройка, четверка и т. д.) и разлагают один из ее цветов на два таким образом, что заменяют его двумя цветами, граничащими с ним с правой и с левой стороны непосредственно (или через одну, две и более промежуточных ступеней). При этом можно цвет сам выключить или оставить расщепленным. Таким же образом можно расщепить и второй цвет. То же можно проделать и с тройками и т. д. Также установки цветов влияют особенно сильно, если они поддерживаются еще и формой расположения цветовых полей, если, например, оба расщепленные цвета расположены зеркально симметрично.

Как видно, число возможностей здесь бесконечно велико, так что скорее опасаешься затеряться в них. Но в этом-то и преимущество научной работы, что она при помощи теории соединений указывает на всевозможные, досягаемые случаи. Этим самым мы доводим их число до максимума, и в то же самое время упорядочиваем их и делаем легко обозримыми. Научную работу здесь можно сравнить с хорошей косильной машиной, которая не только жнет хлеб, но и связывает его в правильные снопы, и правильно разбрасывает эти последние, т. е. дает материал в наилучшей для дальнейшего употребления форме.

До сих пор мы отдельно изучили три большие группы гармонии: ахроматические, однотонные и равнозначные. Попутно, все-таки, было указано на то, что не исключена возможность применения двух или трех видов гармоний в одном и том же цветном предмете. Сейчас же мы и должны подробнее разобрать вопрос о гармониях, составленных таким образом, или же о гармониях второго и высшего порядков.

Мы берем определенный цвет (кусок материи, цвет стены и т. д.) и спрашиваем: какие другие цвета сюда подходят. Эта и есть одна из тех форм, в которой проблема гармоний почти всегда ставится в практике; все остальные формы могут быть приведены к этой путем свободного выбора исходного цвета.

Допустим, что данный цвет соответствует некоторой точке в цветовом теле. Мы проводим через эту точку и ахроматическую ось поверхность и получаем таким образом однотонный треугольник, к коему принадлежит и наш цвет. В этом треугольнике мы проводим через соответствующую цвету точку три линии, параллельные сторонам треугольника, и дающие нам равно-чистые, равно-белые и равно-черные цвета, к которым относится и данная точка нашего цвета. На этих трех прямых и находятся все цвета, которые с данным цветом могут дать однотонные гармонии.

Далее мы проводим через данную точку цвета соответствующий ей равнозначный круг, центр которого совпадает с осью цветового тела; его плоскость перпендикулярна к плоскости треугольника. В этом круге мы находим все цвета, которые могли бы дать равнозначные гармонии с данным цветом.

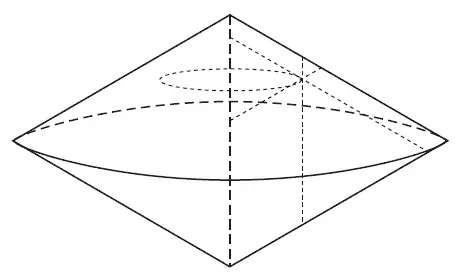
Рис. 40

Три прямых линии в треугольнике перекрещиваются в точке данного цвета и образуют звезду с шестью лучами, не одинаковой длины, конечные точки которых находятся на сторонах треугольника. Перпендикулярно к центру звезды проходит равнозначный круг (см. рис. 40).

Этот круг и звезда содержат все цвета, которые непосредственно гармоничны с данным цветом.

В нашем нормированном цветовом теле это дает всегда 38 цветов, включая и данный цвет, независимо от положения данной цветовой точки а именно: 15 в треугольнике, 24 в круге, где данная точка, однако, считается вторично, так что в сумме получается 38.

Конечно, никогда не приводят одновременно все 38 цветов, также как никогда не нажимают одновременно на все клавиши органа. Все же следует знать, что таковое число дают все цвета, включая сюда и ахроматические, которые образуют с данным цветом полную гармонию; дело обстоит здесь так же, как и в музыке, где при удачном выборе клавишей органа можно воспроизводить любую звуковую гармонию.

Дальнейшее развитие этой простейшей группы гармонии состоит в том, что через каждую из 37 цветовых точек, которые сюда относятся, можно провести новый цветовой круг и получить, таким образом, новые 37 цветов, которые могут образовать с первоначальным цветом гармонию второго порядка. Для того, чтобы это было понятно, должно быть ясно, что здесь мы имеем дело с семейством тех вторых цветов, которые составляют второй круг звезды.