Юрий Артамонов - Ли Смолин. Возрожденное время - От кризиса в физике к будущему вселенной

Рассмотрим пример в двумерном пространстве - а именно, большую область плоскости, как показано на Рис.13. Эта плоскость может иметь квантово-геометрическое описание, изображаемое на рисунке на языке графов. Теперь рассмотри два узла, которые удалены друг от друга на графе на много шагов; мы будем называть их Тед и Мэри. Мы можем сделать новый граф из старого, добавив другое ребро, которое связывает Теда непосредственно с Мэри (см. Рис.16). Это описывает квантовую геометрию, в которой Мэри и Тед являются соседями. Это как если бы они оба просто купили сотовые телефоны; разделяющее их пространство растворяется.

Если геометрия на самом деле квантовая, тогда в нашей наблюдаемой вселенной имеется, возможно, 10180 узлов - то есть, один узел на кубик с ребром Планковской длины. Если каждый соединен только с несколькими ближайшими соседями, то квантовая геометрия на больших масштабах может выглядеть точно подобно классической

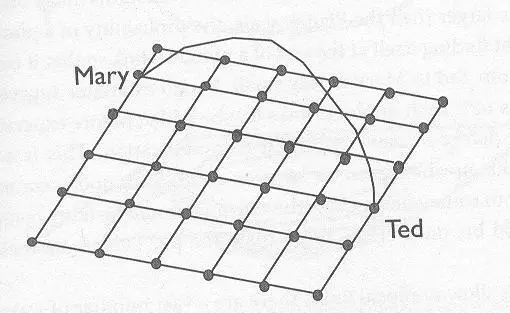Рис.16 . Добавление нелокальной связи нарушает локальность, делая две удаленные точки близкими друг к другу .

к оглавлению

геометрии. Локальность пространства тогда возникает из особого дизайна воспроизводящей его квантовой геометрии. В этом случае, грубо, имеется столько же ребер, сколько и узлов, поскольку каждый узел соединен только с несколькими соседями. Но путем добавления только одного дополнительного ребра к гигантскому числу ребер, составляющих квантовую геометрию, мы разрушаем локальность пространства драматическим образом, делая возможной, по существу, мгновенную коммуникацию между сильно удаленными друг от друга узлами типа Теда и Мэри. Мы называем это нарушением локальности , а добавленное ребро - нелокальной связью [13].

Удивительно легко нарушить локальность, добавив только одну нелокальную связь. Отдельная нелокальная связь будет одной на 10180 ребер внутри наблюдаемой вселенной, но имеется 10360 возможных мест для ее размещения. Если вы добавляете ее в граф с 10180 ребрами случайно, вы намного более вероятно добавите нелокальную связь, чем локальную, поскольку число способов добавить нелокальную связь намного больше, чем число способов добавить ее локально. Узел на одном конце может быть связан с небольшим числом других узлов, если вы хотите создать локальное соединение. Но если вы не заботитесь о локальности, другой конец мог бы зацепить любой узел во вселенной. Вы опять видите, насколько огромным ограничением является локальность.

Вы можете удивиться, насколько много нелокальных связей могло бы быть добавлено к квантовой геометрии пространства, прежде чем мы обратим на это внимание в макромире. Поскольку обычные частицы имеют квантовые длины волн на много порядков больше по величине, чем Планковский масштаб, вероятность фотону видимого света найтись на одном конце нелокальной связи, чтобы он смог перескочить от Теда к Мэри, очень мала. Грубые оценки показывают, что порядка 10100 таких нелокальных связей могут быть добавлены, прежде чем эксперимент будет легко детектировать сверхсветовую коммуникацию. Это огромное число (но даже близко не столь огромное как 10180). Тем не менее, узлы, нелокально соединенные через вселенную с чем-то где-нибудь, будут довольно распространены; в среднем их может быть больше одного на кубический нанометр пространства.

Раз уж мы допустили нелокальные связи, имеется гигантское число способов, которыми локальность может быть нарушена. Вы могли бы также иметь несколько узлов, которые соединены со многими другими узлами. Эти очень общительные узлы могли бы действовать, как

к оглавлению

сплетники действуют в социальной сети, канализируя через вселенную большое количество информации, выступая как кратчайший путь.

Может ли вселенная быть полна таких нелокальных соединений? Как их можно было бы обнаружить?

Очевидная идея в том, что запутывание и другие проявления нелокальности в квантовой теории являются примерами нарушения локальности. Возможно, фундаментальный уровень описания - на котором нет пространства, только сеть взаимодействий, в которой все потенциально связано со всем остальным - представляет собой теорию со скрытыми переменными, доводы в пользу существования которой я приводил в Главе 14. Если это так, то квантовая теория и пространство возникают вместе [14].