Юрий Артамонов - Ли Смолин. Возрожденное время - От кризиса в физике к будущему вселенной

*

Процесс решения обратной проблемы, оказывается, учит нас двум важным урокам в отношении природы времени.

Первый заключается в том, что пространство, более вероятно, должно возникать в моделях квантовой вселенной, которые допускают существование глобальной переменной времени. Это проиллюстрировано моделями динамической триангуляции.

Триангуляция, как отмечалось, это поверхность, построенная из многих соединенных вместе треугольников, как в геодезическом куполе (см. Рис.18). Трехмерное искривленное пространство может быть сконструировано аналогичным образом путем соединения тетраэдров, которые являются трехмерным аналогом треугольников. Модель динамических триангуляций использует эти тетраэдры как атомы пространства. Квантовая геометрия описывается не с помощью графов, а с помощью упорядочения тетраэдров, склеенных лицом к лицу [21]. Такая конфигурация пространства эволюционирует во времени посредством набора правил, чтобы построить дискретную триангулированную версию четырехмерного пространства-времени (см. Рис.20).

Имеется два вида подходов на базе динамических триангуляций: те,

к оглавлению

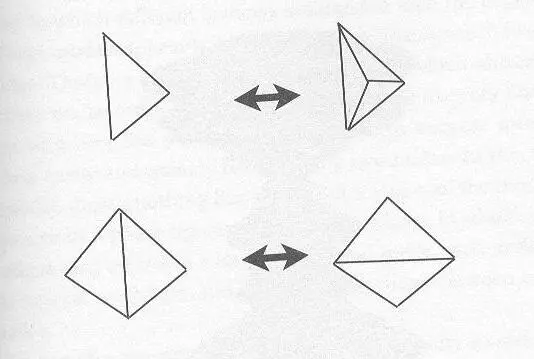Рис.20 . Эволюционные правила для триангуляций поверхностей . в которых пространство-время атомизировано и предполагается возникающим как и в картине монолитной вселенной, и те, в которых допускается универсальное понятие времени, а в качестве возникающего ищется только пространство. Во всем остальном конструкции весьма сходны. Результат таков, что когерентное пространство-время возникает только в моделях, где время предполагается реальным. Другие модели - те, что без глобального времени - пали жертвой обратной проблемы: то есть, они перегружены пагубным влиянием нестандартных геометрий, которые никогда не выглядят подобно пространству (см. Рис.19).

К моделям, решающим обратную проблему, относится модель, известная как причинные динамические триангуляции, изобретенная Амбьорном и Лолл. Эмерджентные варианты пространства-времени в ней частично реалистичны в том, что они имеют три размерности пространства и одну времени; некоторые из них показаны на Рис.21. Они являются первым примером квантовых вселенных, которые на больших масштабах выглядят как решения ОТО Эйнштейна. Они даже демонстрируют, что объем пространства растет во времени тем же образом, который требуют уравнения Эйнштейна.

Тут остаются некоторые вопросы, требующие решения - например, похожи ли эти эмерджентные варианты пространства-времени на решения ОТО в достаточных деталях, чтобы воспроизвести такие явления как гравитационные волны и черные дыры. Другим вызовом является понять судьбу встроенного в модели понятия глобального времени. А также старый вопрос, нарушает ли

к оглавлению

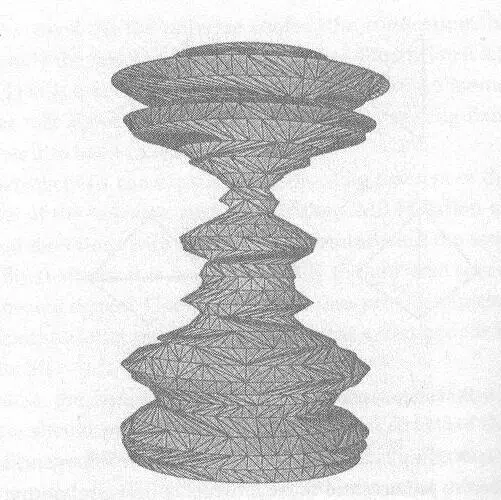Рис.21 . Типичная пространственно-временная геометрия, возникающая из модели причинных динамических триангуляций [22] . присутствие глобального времени многозначно установленную временную симметрию ОТО (см. Главу 6). Новый способ задать этот вопрос: является ли ОТО - или может ли быть благодаря некоторой адаптации модели - восстановленной в виде динамики формы, которая, как мы видели в Главе 14, является теорией с глобальным временем, эквивалентной ОТО.

Второй урок в том, что если пространство эмерджентно, то на самом глубоком уровне не может быть относительности одновременности, поскольку все соединено со всем остальным. Поскольку мы можем послать сигнал между любыми двумя узлами в один или несколько шагов, тут нет проблемы синхронизированных часов. Отсюда следует, что на данном уровне время должно быть глобальным.

Этот урок иллюстрируется результатами моделей квантовых граффити. Здесь местом действия является граф с большим числом узлов, из которых любые два или соединены или нет. Квантовые геометрии тогда включают любой граф, в котором можно сделать соединенными все узлы. Динамический закон включает или выключает соединения. Изучались некоторые модели,

к оглавлению

в которых предлагались различные законы для включения и выключения ребер. Эти модели, как оказывается, имеют две фазы, аналогичные двум фазам воды. Это высокотемпературная фаза, в которой почти все ребра включены, так что каждый узел тесно связан с каждым другим узлом в один или немного шагов. Тут нет локальности, поскольку информация может легко и быстро перескакивать между любыми двумя узлами. В этой фазе модели нет ничего похожего на пространство. Но если вы охлаждаете модель, проявляется фазовый переход к замороженной фазе, в которой почти все ребра отключены. Как и в низкоразмерном пространстве, каждый узел имеет только несколько ближайших соседей, и требуется много перескоков между большинством пар узлов.