Юрий Артамонов - Ли Смолин. Возрожденное время - От кризиса в физике к будущему вселенной

к оглавлению

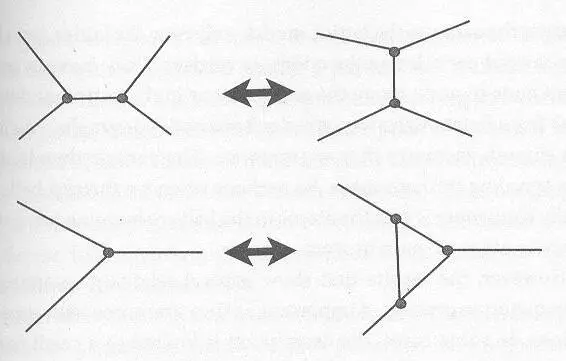Рис.15 . Правила, по которым графы эволюционируют во времени в петлевой квантовой гравитации. Каждый кадр может служить малой частью графа, как показано на рисунке .

ее к ОТО является упражнением, требующим в техническом смысле напряжения сил, но после ее аккуратного проведения она приводит к картине, которую мы здесь описали, с точными правилами для изменения графов во времени. Таким образом, мы называем петлевую квантовую гравитацию 'квантованием' ОТО [10].

В качестве альтернативы мы можем стартовать с квантовых правил для изменения графов и поинтересоваться, могут ли правила классической ОТО быть выведены как приближение к квантовым правилам. Это аналог вывода уравнений, которые описывают течение воды из фундаментальных законов, которым подчиняются атомы, составляющие воду. Это упражнение называется выводом классической теории из классического предела квантовой теории. Это сложно, но с недавних пор имеются положительные результаты в петлевой квантовой гравитации [11]. Они использовали пространственно-временной подход к квантовому пространству-времени, именуемому моделью спиновой пены, в которой сеть, лежащая в основе геометрии пространства, рассматривается как часть большей сети, охватывающей пространство и время. Отсюда спиновая пена дает квантовую версию картины монолитной вселенной, в которой пространство и время объединены в единую структуру. Что особенно впечатляет, так это что имеются некоторые независимые результаты, показывающие возникновение ОТО из моделей спиновой пены.

Легко добавить в картину квантовой геометрии даже материю. История

к оглавлению

та же, что и в модели решетки, только теперь решетка может изменяться. Мы можем вставлять частицы в узлы или вершины. Они двигаются, прыгая от узла к узлу вдоль ребер, точно так же, как и в модели решетки. Если вы посмотрите в достаточной степени издалека, вы не увидите узлы и графы, вы увидите только гладкую геометрию, которая их аппроксимирует. Частицы тогда будут выглядеть, как будто они путешествуют через пространство. Так что возможно, что когда мы кидаем мяч, на самом деле происходит то, что атомы в мяче перепрыгивают от атома пространства к атому пространства и к атому пространства.

Однако, результаты, которые показывают, что ОТО возникает из петлевой квантовой гравитации, как бы важны они ни были, достигаются с некоторыми ограничениями. В некоторых случаях описание ограничено малой областью пространства-времени, окруженной границей. Наличие границы говорит нам, что петлевая квантовая гравитация лучше понимается как описание малой области пространства-времени, и поэтому соответствует Ньютоновской парадигме.

Имеются также результаты в теории струн, наводящие на мысль, что пространство-время может появляться в ограниченной области - по меньшей мере, когда космологическая константа принимает отрицательное значение. Они возникают в контексте дуальности между ОТО и масштабно-инвариантной теорией, гипотезу о которой высказал Хуан Малдасена, о чем я упоминал в Главе 14. Если эта гипотеза верна - а многие результаты ее поддерживают - тогда классическое пространство-время может появляться во внутренней области, граница которой имеет фиксированную классическую геометрию.

Таким образом, и петлевая квантовая гравитация и теория струн намекают, что квантовая гравитация может быть понята как описание областей пространства-времени с границами, поэтому укладывается в рамки Ньютоновской парадигмы. Их самые сильные результаты достигнуты в контексте физики в ящике, без обращения к проблеме, может или не может описание быть масштабировано к теории целой замкнутой вселенной.

Другое допущение при получении результатов петлевой квантовой гравитации о появлении пространства-времени заключается в том, что графы, описывающие квантовую геометрию пространства, ограничены тем, что уже выглядит как дискретная картина низкоразмерного пространства [12]. В этих случаях локальность пространства фиксируется тем, что каждая вершина или узел графа соединяется только с небольшим числом других вершин. Точно как в загородном

к оглавлению

поселке, каждый узел имеет только несколько ближайших соседей. Чтобы пропутешествовать между широко разнесенными узлами, частица должна сделать много перескоков. Для преодоления длинного пути для частицы или для квантового переноса информации требуется время. Поэтому возникает описание мира с конечной скоростью света. Однако, имеется много состояний квантовой геометрии, в которых нет хорошей версии локальности. Имеются графы, в которых каждый узел связан с каждым другим узлом только через несколько шагов. До сегодняшнего дня методы петлевой квантовой гравитации не прояснили, как развиваются такие квантовые геометрии.