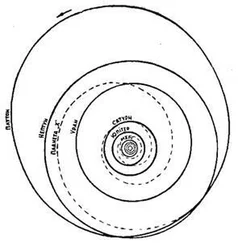
Окремо слід зауважити: ніхто із знавців фізики не міг заперечити формул по суті — від них просто відмахувались як від чогось такого, що перебуває за межами фізичної реальності. Приблизно так, як від перпетуум-мобіле.
Ось чому з’явився цей роман: автор за його допомогою прагне розкрити філософську сутність субстанціональної фізики — тобто такої фізики, яка перебуває на грані фізичного й метафізичного. Час її народження вже наспів. Кому ця ідея не до вподоби, той знайде дуже простий вихід — відкине геть цю книгу. Автор, чемно вклонившись, погодиться з такою критикою: читач завжди правий. (Прим. автора).
Тепер, коли читачеві відома Сила Моносу як С 4/G, ми, використавши формулу 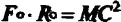 , зможемо переписати ньютонівський закон всесвітнього тяжіння на радіуси монад:
, зможемо переписати ньютонівський закон всесвітнього тяжіння на радіуси монад:
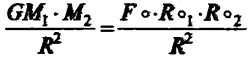
Імпульс на квантовому рівні виглядає так: 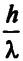 , де λ — довжина хвилі, h — стала Планка, поділена на 2 π . Підставивши цей вираз у формулу імпульсу монади, дістанемо:
, де λ — довжина хвилі, h — стала Планка, поділена на 2 π . Підставивши цей вираз у формулу імпульсу монади, дістанемо: 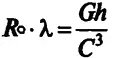 . Величини
. Величини 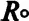 і λ мають ту саму розмірність, отже: см2. Звідси й отримуємо квант простору. Або, кажучи інакше, ми дістали найменшу просторову константу. Це, безумовно, світова константа, бо ми її отримали із трьох відомих світових констант. Радіуси атомних монад іще менші, але ж до світових констант вони не належать — вони є константами лише в межах своїх власних систем. (Прим. автора).
і λ мають ту саму розмірність, отже: см2. Звідси й отримуємо квант простору. Або, кажучи інакше, ми дістали найменшу просторову константу. Це, безумовно, світова константа, бо ми її отримали із трьох відомих світових констант. Радіуси атомних монад іще менші, але ж до світових констант вони не належать — вони є константами лише в межах своїх власних систем. (Прим. автора).
Українська Радянська Енциклопедія, т. 14, с. 143. — К., 1963.
Московська газета «За рубежом» (1978, ч. 24) передрукувала повідомлення із лондонської газети «Нью сайєнтист», в якому обстоюються згадані твердження. Вони повторюються в багатьох інших виданнях. (Автор).
Загальна маса нашої Галактики становить 2×10 44 г ; отже, її загальна енергія ( MС 2 ) дорівнює 1,8×10 65 ергів . За формулою Сили Моносу, радіус живої плоті нашої Галактики має дорівнювати:
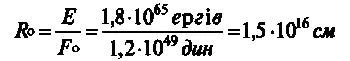
Якщо всю масу Галактики вписати в цей радіус, то густина живої плоті (монади) повинна становити:
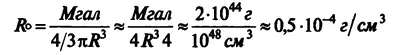
У правій частині немає мас — є лише просторові величини й Сила Моносу. В лівій частині бачимо закон всесвітнього тяжіння в його традиційному вигляді. Неважко упевнитися, що ліва й права частини цілком дорівнюють одна одній. Докір може бути лише такий: надто незручно оперувати величинами правої частини — в ньютонівському варіанті все це виглядає простіше й наочніше. Але ж не забуваймо, що природі байдуже до наших зручностей і наочності формул: вона живе в собі й для себе, незалежно від того, що ми про це думаємо. Крім того, права частина подається нами лише заради гносеології, але ж не заради фізичної практики. Слід мати на увазі, що радіуси монад ( 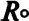 1і
1і 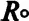 2) належать масам М 1і М 2.
2) належать масам М 1і М 2.
Із лівої частини напрошується висновок, що маси тяжіють одна до одної. Це, можна сказати, буденна очевидність, котра всюди піддається спостереженням, і через те вона здобула перемогу. Динаміка правої частини може бути витлумачена цілком протилежно: монади небесних тіл, що дірявлять, розсовують простір, мов металеві кульки, втиснуті в гуму, не тяжіють одна до одної, а навпаки — відштовхуються; проте всесвітня переповненість монадами змушує слабкіші з них прилучатися до сильніших, віддаючи власну енергію центрові системи. Цей процес глибоко схований від спостерігача, як і самі монади.
Із правої й лівої частин розглянутого рівняння можна отримати дещо позірно схоже на закон всесвітнього тяжіння, але зовсім не схоже за внутрішнім змістом:
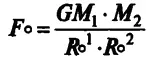
Тут ми наочно бачимо, як Сила Моносу ( 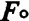 ) розщеплюється на складники, але ж загалом лишається сама собою, — це вона зганяє монади докупи, мов чабан зганяв овець. А коли монади розійдуться на значну відстань (вони для нас виглядатимуть небесними тілами), Сила Моносу перетвориться на ньютонівську силу тяжіння. Та чи перестане вона бути Силою Моносу?..
) розщеплюється на складники, але ж загалом лишається сама собою, — це вона зганяє монади докупи, мов чабан зганяв овець. А коли монади розійдуться на значну відстань (вони для нас виглядатимуть небесними тілами), Сила Моносу перетвориться на ньютонівську силу тяжіння. Та чи перестане вона бути Силою Моносу?..
Читать дальше

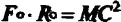 , зможемо переписати ньютонівський закон всесвітнього тяжіння на радіуси монад:
, зможемо переписати ньютонівський закон всесвітнього тяжіння на радіуси монад: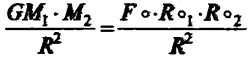
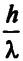 , де λ — довжина хвилі, h — стала Планка, поділена на 2 π . Підставивши цей вираз у формулу імпульсу монади, дістанемо:
, де λ — довжина хвилі, h — стала Планка, поділена на 2 π . Підставивши цей вираз у формулу імпульсу монади, дістанемо: 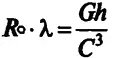 . Величини
. Величини 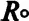 і λ мають ту саму розмірність, отже: см2. Звідси й отримуємо квант простору. Або, кажучи інакше, ми дістали найменшу просторову константу. Це, безумовно, світова константа, бо ми її отримали із трьох відомих світових констант. Радіуси атомних монад іще менші, але ж до світових констант вони не належать — вони є константами лише в межах своїх власних систем. (Прим. автора).
і λ мають ту саму розмірність, отже: см2. Звідси й отримуємо квант простору. Або, кажучи інакше, ми дістали найменшу просторову константу. Це, безумовно, світова константа, бо ми її отримали із трьох відомих світових констант. Радіуси атомних монад іще менші, але ж до світових констант вони не належать — вони є константами лише в межах своїх власних систем. (Прим. автора).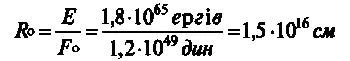
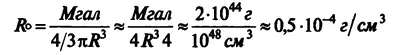
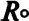 1і
1і 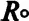 2) належать масам М 1і М 2.
2) належать масам М 1і М 2.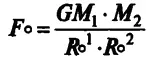
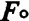 ) розщеплюється на складники, але ж загалом лишається сама собою, — це вона зганяє монади докупи, мов чабан зганяв овець. А коли монади розійдуться на значну відстань (вони для нас виглядатимуть небесними тілами), Сила Моносу перетвориться на ньютонівську силу тяжіння. Та чи перестане вона бути Силою Моносу?..
) розщеплюється на складники, але ж загалом лишається сама собою, — це вона зганяє монади докупи, мов чабан зганяв овець. А коли монади розійдуться на значну відстань (вони для нас виглядатимуть небесними тілами), Сила Моносу перетвориться на ньютонівську силу тяжіння. Та чи перестане вона бути Силою Моносу?..