Слід звернути увагу ось на що: якби довжина гравітаційного радіуса в загальній теорії відносності вимірювалась не за формулою 2GM / С 2 , а за формулою GM / С 2 , то поміж гравітаційним радіусом ( Rg ) і радіусом живої плоті ( 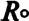 ) можна було б поставити знак рівності.
) можна було б поставити знак рівності.
Деякі фізики-теоретики вважають, що двійка у формулі Ейнштейна виникла із непослідовності в розрахунках. Ось що з цього приводу пише визначний фізик-теоретик В. Л. Гінзбург:
«Розрахунок цей виглядає непослідовно бодай тому, що фактично для тіл зі швидкістю, порівняною зі швидкістю світла С , кінетична енергія дорівнює 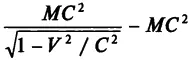 , а не МС 2/ 2 Якщо в наведеному розрахунку вважати енергію корпускули рівною МС 2 , то для Rg ми одержали б значення GM / С 2 .» (В. Л. Гінзбург. О физике и астрофизике. — Москва: Наука, 1980. — С. 111).
, а не МС 2/ 2 Якщо в наведеному розрахунку вважати енергію корпускули рівною МС 2 , то для Rg ми одержали б значення GM / С 2 .» (В. Л. Гінзбург. О физике и астрофизике. — Москва: Наука, 1980. — С. 111).
Але ці відмінності в формулах не такі значні, щоб можна було пояснити, чому в галактичних «чорних дірах» астрофізики вбачають фантастичну густину, яка буцімто дорівнює мільярдам тонн в одному кубічному сантиметрі.
Тепер слід звернути увагу на інше: ґрунт, на якому виростає формула Сили Моносу, можна вбачати в двох парадоксах Ейнштейна — в його непослідовності щодо постулату Шварцшильда й непослідовності в розрахунках, про які щойно йшлося (прим, автора).
— Цілком правильно, — вдоволено підхопив Грива. — Саме так!.. Сучасна фізика, намагаючись описати центри галактик, оперує формулою, яка складається із таких констант: сім кіп гречаної вовни.
— Це вже ви занадто! Фізики оперують теорією відносності.
— А ви чим оперували? І результат вийшов цілком протилежний. Отже, тут справа не в самій теорії відносності, а в тому, що її можливості вичерпуються раніше, ніж ми опиняємося в центрі космічної системи. Саме через те й виникла проблема сингулярності.
— Гаразд. Поясніть, як ви уявляєте центр Галактики.
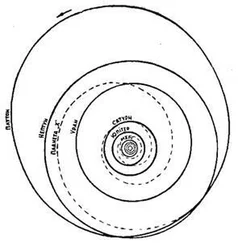
Іван Корнійович, кинувши це запитання, напружено стежив за обличчям Гриви. А той, мабуть, і сам не знав, як міняється його обличчя, коли він подумки переселяється в галактичний центр — туди, де астрофізики поселили «чорну діру». Чорна вона тому, що там таке велике тяжіння, яке не дає змоги пробитися назовні поза її оболонку жодному променеві. А «діра» тому, що надмірне тяжіння буцімто безперервно втягує в себе проміння довколишніх зірок, мов велетенський насос втягує воду. Але ж не можна вічно втягувати й нікуди не викидати! Отож, мабуть, викидає — але куди? Тут і з’являється: у сусідній всесвіт. Де ж він міститься? Не інакше як у напрямі до центру Галактики, бо в напрямі від центру ми потрапляємо в той Всесвіт, у якому живемо самі.
Ні, Грива не приймає такої моделі. Та модель центру Галактики, яка живе в його уяві, не просто інша — вона є могутнім осередком живої плоті, що за своїми розмірами перевершує діаметр Сонячної системи. Ось чому на запитання Жовтого він урочисто, навіть побожно відповів:
— То є Світло, в якому немає жодної темряви.
Жовтий поблажливо усміхнувся:
— Мені ви можете це казати, але комусь іншому не раджу… Так Іоанн Богослов визначає сутність Бога.
Мирон Сидорович струснув довгим волоссям.
— І правильно визначає!
— Можливо. Але ж ми з вами умовились обговорювати фізичну модель світу.
Грива підвівся з крісла, наблизився до вікна. Його огрядна постать кинула розріджену тінь на обличчя співрозмовника.
— Саме фізичну модель я й маю на увазі. Зовнішня оболонка галактичної монади міститься там, де гравітаційний потенціал сягає квадрата швидкості світла. Далі, в глибину монади, ми маємо цілком однорідне середовище. Там уже зовсім немає тяжіння. Уявлення про безмежне зростання гравітаційних сил до центру системи — це помилка! І дуже велика. Саме вона докорінно спотворює…
Іван Корнійович згідливо похитав головою, даючи зрозуміти, що не варт розжовувати те, що й так ясно. Він сказав:
— Якщо з’являється скінченна сила, безмежне зростання гравітаційних сил виключається. Отже, ви гадаєте, що в центрі Галактики є надзвичайно розріджене ядро?.. Даруйте, це дуже важко уявити. Але розрахунки справді показують, що в ядрі Галактики ми маємо трохи не вакуум. І це замість речовини, в якій кожен кубічний сантиметр важить кілька мільярдів тонн. Помилка просто фантастична! Але хто ж помиляється?..
— Ми з вами разом обчислювали.
Читать дальше

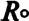 ) можна було б поставити знак рівності.
) можна було б поставити знак рівності.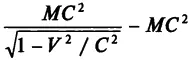 , а не МС 2/ 2 Якщо в наведеному розрахунку вважати енергію корпускули рівною МС 2 , то для Rg ми одержали б значення GM / С 2 .» (В. Л. Гінзбург. О физике и астрофизике. — Москва: Наука, 1980. — С. 111).
, а не МС 2/ 2 Якщо в наведеному розрахунку вважати енергію корпускули рівною МС 2 , то для Rg ми одержали б значення GM / С 2 .» (В. Л. Гінзбург. О физике и астрофизике. — Москва: Наука, 1980. — С. 111).