Дуглас Хаббард - Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе]

1) вы получите 1000 дол., если год публикации книги Ньютона окажется в пределах между верхней и нижней границами указанного вами интервала. Если границы выбраны неверно, то не выиграете ничего;

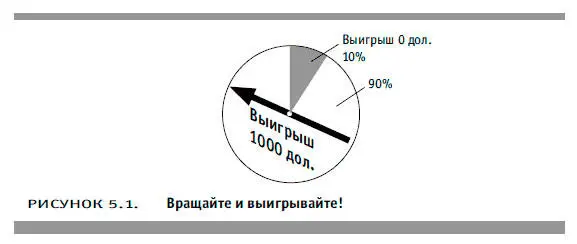
2) вы должны раскрутить круглый диск, разделенный на два неравных сектора, площади которых составляют 90 и 10 % соответственно. Если указатель остановится на большем секторе диска, то вы выиграете 1000 дол., если же на меньшем, то не выиграете ничего (то есть вероятность выигрыша — 90 %).

Какой из вариантов вы выберете? Во втором случае шанс выиграть составляет 90 %. Если вы такой же, как большинство (примерно 80 %) людей, то предпочтете вращать диск. Но почему? Единственным объяснением может служить ваша убежденность в том, что шансов выиграть, раскручивая диск, гораздо больше. Отсюда вывод: доверительный интервал с вероятностью 90 % на самом деле — неправильная оценка, сделанная вами. Эта вероятность, скорее, составляет 80, 65, а то и 50 %. С точки зрения статистики это называется чрезмерной уверенностью. Вы выразили неопределенность таким образом, который указывает на гораздо меньшее ее значение по сравнению с фактическим.

Так же нежелателен выбор варианта 1, в котором вы получите 1000 дол., если указанный год попадет в границы вашего интервала. Данный выбор демонстрирует, что на самом деле вы уверены в своем ответе более чем на 90 % (хотя и указали, что убеждены в нем именно на 90 %).

Правильный ответ в данном случае — сказать, что ни один из вариантов не является предпочтительным. Так вы покажете, что уверены в своем ответе именно на 90 % (а не на больше или меньше). Но для этого тем, кто слишком уверен в себе (то есть большинству из нас), пришлось бы предварительно расширить свой доверительный интервал.

То же проверочное упражнение можно проделать и с бинарными вопросами. Допустим, что вы на 80 % уверены в правильности своего ответа на вопрос о месте рождения Наполеона. Сделайте снова выбор между способами получения приза (1 или 2). Но пусть в этом случае вероятность выигрыша при вращении диска будет составлять только 80 %. Если вы предпочтете раскручивать диск, значит, уверены в своем ответе менее чем на 80 %. Пусть вероятность выигрыша при вращении диска сократится до 70 %. Если вы и в таком случае сделаете этот выбор, то действительно убеждены в своей правоте только на 70 %.

На тренингах по калибровке я называю такую процедуру проверкой с помощью эквивалентных ставок. Как видно из самого названия, она помогает установить, действительно ли вы на 90 % уверены в названном интервале значений, предлагая сделать другую ставку, представляющуюся эквивалентной. Исследования показывают: даже когда люди только воображают, что рискуют деньгами, это значительно улучшает их способность оценивать шансы [20] Ibid. . На деле же выяснилось, что, реально рискуя деньгами, они оценивают шансы лишь ненамного точнее, чем когда рискуют ими понарошку (подробнее об этом в той части главы 13, где обсуждаются рынки предсказаний).

Методы, подобные проверке с помощью эквивалентных ставок, помогают людям точнее оценивать неопределенности. Тех, кто точно определяет степень своей уверенности (то есть тех, кто оказывается прав в 80 % случаев, когда говорит, что уверен на 80 %), называют калиброванными специалистами. Существуют и другие простые приемы подготовки калиброванных экспертов, но давайте сначала посмотрим, как вы справились с этим тестом. Ответы даны в приложении А.

Чтобы понять, насколько вы калиброваны, необходимо сравнить ожидаемые вами результаты с фактическими. Поскольку вас просили указать 90-процентный CI, вы, в сущности, полагаете, что 9 из 10 правильных ответов окажутся в названных вами интервалах значений. Однако если вы похожи на большинство людей, то процент «прямых попаданий», скорее всего, окажется меньше. Конечно, это очень малые выборки, не позволяющие точно оценить вашу калибровку, но примерное представление они дают. Если даже при такой малой выборке в ваши доверительные интервалы попали менее семи верных ответов, вы, скорее всего, страдаете преувеличенной уверенностью. А когда их оказывается менее пяти (как у большинства людей), вы чрезмерно самонадеянны.

Итак, отвечая на вопросы с 90-процентным доверительным интервалом, вы ожидали, что в предложенные вами границы попадут девять правильных ответов, но фактически их оказалось меньше. Теперь необходимо определить «ожидаемые» значения для бинарных вопросов. Вы указали, что уверены в своих ответах на каждый из них на 50, 60, 70, 80, 90 или 100 %. Переведите все обведенные вами кружочком проценты в десятичные дроби (0,5; 0,6… 1,0) и суммируйте их. Предположим, что вы были уверены в своих ответах на 1,0; 0,5; 0,9; 0,6; 0,7; 0,8; 0,8; 1,0; 0,9 и 0,7, тогда сумма этих показателей составляет 7,9. Таким образом, «ожидаемый» показатель равен 7,9. Конечно, 10 — тоже небольшая выборка, но если ваш фактический показатель составил, например, 2,5, то, скорее всего, вы слишком самонадеянны.