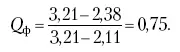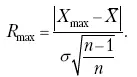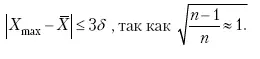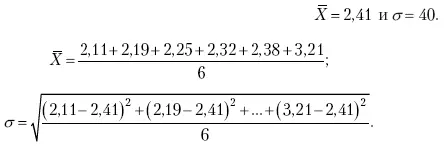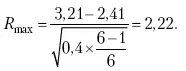Леонид Букин - Статистика - учебное пособие

Однако в совокупности могут встречаться отдельные единицы, у которых t > 3. Это будет свидетельствовать о неоднородности совокупности, и такие единицы совокупности целесообразно исключить как аномальные, нетипичные для данной совокупности.

Если совокупность мала (3 ≤ n ≤ 8), то однородность совокупности, т. е. проверку годности первичных данных, можно осуществить следующим образом. Вычисляют показатель, характеризующий отношение разности между сомнительным и соседним значениями ранжированного в порядке возрастания ряда к разности между крайними значениями, т. е.:

если вызывает сомнение первое в ряду значение признака, и:

если вызывает сомнение последнее в ряду значение признака.

Вычисленную величину Q сопоставляют с табличным ее значением для данного числа наблюдений и уровня вероятности. Если Q ф> Q табл, то сомнительное значение следует исключить из обработки. Если же Q ф< Q табл, то сомнительное значение не отбрасывается. Рассмотрим эту методику на примере.

Допустим, получены следующие результаты содержания золы в образцах корма в процентах: 2,25; 2,19; 2,11; 2,38; 2,32 и 3,21.

Располагаем данные анализа в порядке возрастания их значений: 2,11; 2,19; 2,25; 2,32; 2,38; 3,21.

Вычисляем:

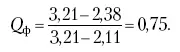
Далее находим Q таблдля n = 6 и вероятности p = 0,99 (табл. 4).

Таблица 4. Значения Q в зависимости от степени надежности (p)

и общего числа значений признака (n)

Величина Q табл= 0,70. Следовательно, значение 3,21 должно быть исключено как нетипичное для данной совокупности.

При числе значений признака больше трех (и больше восьми) можно использовать другую методику определения пригодности первичных данных. По всем значениям признака в совокупности сначала рассчитывают среднюю величину (Х) и среднее квадратическое отклонение (σ), затем на основании разницы (без учета знака) между максимально отклоняющимся значением (X max) и средней величиной находят величину критерия R maxпо формуле:

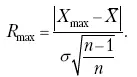
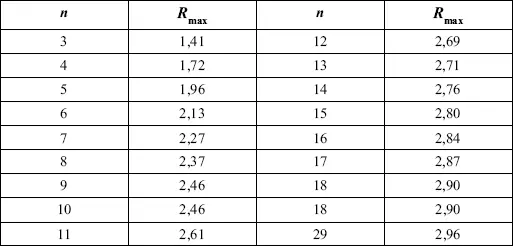
Значение R maxсопоставляют с табличным его значением при данном числе значений признака для вероятности p = 0,99 (табл. 5).

Если R max > R табл, то сомнительное значение (X) следует исключить, если же R max< R табл, то значение (X max) следует принимать в расчет.

При n > 20 показатель R max≈ 3 и условие пригодности имеет вид:

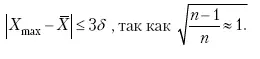
Таблица 5. Значения R max для степени надежности p = 0,99 в зависимости

от числа единиц совокупности n

Обратимся к предыдущему примеру и вычислим:

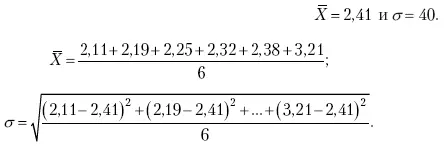
При расчете средней величины и среднего квадратического отклонения используют все значения признака. Затем рассчитываем:

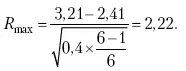
Для n = 6, R табл_ 2,13; так как 2,22 > 2,13, то сомнительное значение 3,21 необходимо отбросить из статистической обработки. Если сомнение вызывает не одно, а несколько значений, то сначала производят указанные выше расчеты только для одного из них (наиболее отклоняющегося). После его исключения повторяют расчет для следующего сомнительного значения, вычисляя заново X и σ.

При проверке годности данных с использованием любой методики может быть исключено не более одной трети единиц совокупности.

Если исключению подлежит более одной трети всех единиц совокупности, то данная совокупность считается неоднородной.

При изучении экономических явлений статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупностей. Величины признаков варьируют под воздействием различных причин и условий. Чем разнообразнее условия, влияющие на размер признака, тем больше его вариация.