Леонид Букин - Статистика - учебное пособие

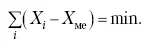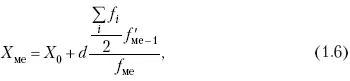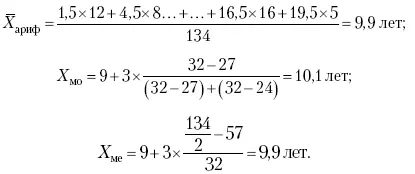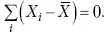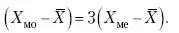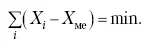
Это свойство имеет большое значение для решения некоторых практических задач – например, для расчета самого короткого из всех возможных расстояний для разных видов транспорта, для размещения станций техобслуживания таким образом, чтобы расстояние до всех обслуживаемых данной станцией машин было минимальным, и т. п.

При отыскании медианы сначала определяется ее порядковый номер в ряду распределения:

Далее, соответственно порядковому номеру, по накопленным частотам ряда находят саму медиану. В дискретном ряду – без всякого расчета, а в интервальном ряду, зная порядковый номер медианы, по накопленным частотам отыскивается медианный интервал, в котором путем простейшего приема интерполяции определяется уже значение медианы. Расчет медианы осуществляется по формуле:

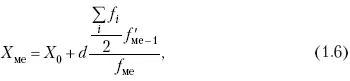
где Х 0 – нижняя граница медианного интервала; d – величина интервала; f _ 1– частота, накопленная до медианного интервала; f – частота медианного интервала.

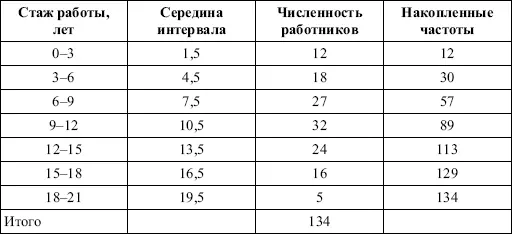
Рассчитаем среднюю величину, моду и медиану на примере интервального распределения. Данные приведены в табл. 2.

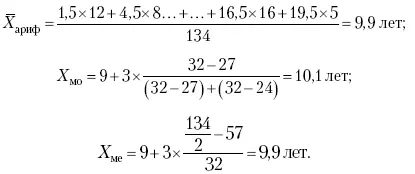
Таким образом, в качестве центра распределения могут быть использованы различные показатели: средняя величина, мода и медиана,

и каждая из этих характеристик имеет свои особенности. Так, для средней величины характерно то, что все отклонения от нее отдельных значений признака взаимно погашаются, т. е.

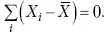
Для медианы характерно то, что сумма отклонений индивидуальных значений признака от нее (без учета знаков) является минимальной. Мода же характеризует наиболее часто встречающееся значение признака. Поэтому в зависимости от того, какая из особенностей интересует исследователя, и должна выбираться одна из рассмотренных характеристик. В отдельных случаях рассчитываются все характеристики.

Их сравнение и выявление соотношений между ними помогает выяснить особенности распределения того или иного вариационного ряда. Так, в симметричных рядах, как в нашем случае, все три характеристики (средняя, мода и медиана) примерно совпадают. Чем больше расхождение между модой и средней величиной, тем более асимметричен ряд. Установлено, что для умеренно асимметричных рядов разность между модой и средней арифметической примерно в три раза превышает разность между медианой и средней арифметической:

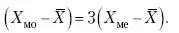
Это соотношение можно использовать для определения одного показателя по двум известным. Из этого следует, что сочетание моды, медианы и средней важно и для характеристики типа распределения.

Статистическое описание совокупности было бы неполным, если ограничиться лишь показателями центральной тенденции, т. е. средними величинами, модой и медианой, которые являются равнодействующими ряда изменяющихся значений признака. В одних случаях значение признака концентрируется возле некоторого центра очень тесно, в других случаях наблюдается значительное рассеивание, хотя средняя величина может быть одинаковой. В связи с этим средняя величина как показатель центральной тенденции не дает исчерпывающей характеристики изучаемой совокупности. Возникает необходимость изучения характера рассеивания признака. Хотя отклонения от средней и регулируются общими для всех единиц совокупности причинами, формирующими среднюю, но в то же время они обусловлены и индивидуальными причинами. Например, отклонения производительности труда отдельных рабочих, работающих в одной бригаде, а стало быть, находящихся в одинаковых условиях труда, вызваны не общими условиями и причинами, а индивидуальными обстоятельствами рабочих и их квалификацией, состоянием здоровья, настроением, сообразительностью и т. д. Поэтому изучение отклонений от средней их размеров и закономерности распределения представляет большой интерес для исследователя. Это важно прежде всего для оценки однородности совокупности, которую характеризует данная средняя величина, так как для качественно однородной совокупности характерна вариация в определенных границах. Стало быть, чем меньше вариация, тем качественно однороднее совокупность, тем типичнее и объективнее средняя величина, характеризующая ее.