13.5.1. Уравнения для розничной торговли
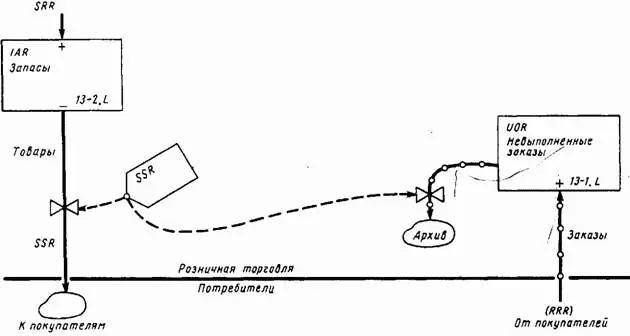
Рис. 13-2. Исходная диаграмма потоков в розничной торговле.
Мы начнем с двух простых уравнений: одно описывает уровень невыполненных заказов, другое — запасы товаров. На рис. 13-2 показаны эти две переменные на первой стадии построения диаграммы потоков. Здесь IAR — запасы товаров, а сплошные линии изображают входящие и исходящие потоки материалов; UOR — уровень невыполненных заказов; соответствующие потоки изображены линиями с кружками, идущими к прямоугольнику и от него. Величина UOR может быть определена с помощью обычного уравнения уровня, который зависит от темпов одного входящего и одного исходящего потоков [67] Сущность уравнений, описывающих уровни, рассматривалась в главе 6.
.
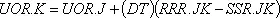 ,
,
13-1,
L
где
UOR — заказы, не выполненные розницей (в единицах товара);
RRR — требования (заказы), получаемые розницей (единицы в неделю);
SSR — розничная отгрузка (единицы в неделю);
DT — интервал времени между решениями уравнений (недели).
В указанном справа порядковом номере уравнения цифра 13 означает номер, главы цифра 1 — номер уравнения внутри главы, а индекс L указывает, что это уравнение описывает уровень. Уравнение определяет количество невыполненных заказов в настоящий момент времени К, исходя из количества невыполненных заказов, определенного в последний раз для момента времени Y , и из темпов входящего и исходящего потоков в интервале времени JK между вычислениями. Темпы входящих и исходящих потоков в течение интервала JK принимаются постоянными (для того, чтобы это допущение было приемлемым, интервал времени должен быть достаточно коротким). Произведение продолжительности интервала времени DT на темп входящего потока RRR. JK определяет число новых заказов, полученных за интервал JK. Точно так же произведение (DT)(SSR.JK) определяет количество заказов, выполненных в течение этого же интервала. Обе части уравнения имеют одинаковую размерность:
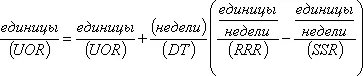
Интервал времени между решениями DT должен быть коротким по сравнению с величиной отображаемых в модели запаздываний [68] См. раздел 6.5.
. В нашем примере интервал решений должен быть небольшой частью недели. Темпы потока при такой формулировке уравнения измеряются в общепринятых единицах (например, недельный темп), и уравнение остается справедливым независимо от длины интервала DT. Это оставляет достаточную свободу для выбора интервала времени DT между решениями в соответствии с критериями, которые будут рассмотрены ниже.
На рис. 13-2 для полноты учета всех видов потока показан архив выполненных заказов, исключаемых из действующей системы.
Второе уравнение, описывающее уровень запасов в розничной торговле, по существу аналогично первому:
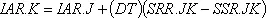 ,
,
13-2,
L
где
IAR — фактический запас в рознице (единицы);
SRR — поставки, получаемые розницей (единицы в неделю);
SSR — розничная отгрузка (единицы в неделю).
Приведенные уравнения, описывающие уровни, просты и неопровержимы. Они представляют собой основу описания системы. Эти уравнения отражают тот факт, что действительный остаток определяется путем последовательного прибавления или вычитания количеств, определяемых темпами входящего и исходящего потоков.
Уравнения темпов, напротив, не являются столь очевидными и простыми. Именно в уравнениях темпов отображается механизм решений, свойственный системе. Уравнения темпов отражают наше понимание факторов, определяющих действия. Решения, которые регулируют темпы и лежат в основе уравнений темпов, должны быть сформулированы таким образом, чтобы уравнения оставались справедливыми и достаточно точными при любых, даже самых больших изменениях значений переменных, которые могут иметь место в системе. Уравнения темпов часто включают нелинейные функциональные зависимости, описывающие реальное поведение системы в различных обстоятельствах.
Читать дальше

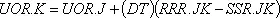 ,
,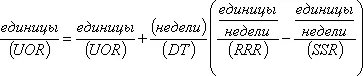
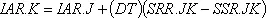 ,
,






![Джей Джей Барридж - Секрет рапторов [litres]](/books/420944/dzhej-dzhej-barridzh-sekret-raptorov-litres-thumb.webp)



