Джей Форрестер - Основы кибернетики предприятия

Сила воздействия функций решения.Динамическое поведение информационной системы с обратной связью определяется тем, каким образом изменения в одной переменной приводят к изменениям в другой. Анализ этого вопроса может привести к предположению о высокой чувствительности системы к точности параметров [47] Параметр — это постоянная для данного цикла работы модели величина, которая была определена при конструировании модели. Разумеется, она может быть изменена для того или иного периода работы. в функциях решений, однако обычно это не так.

Если модель сконструирована правильно и она выражает действительную структуру социальной системы с обратной связью, то она будет обладать такой же способностью самокорректировки, как в реальных жизненных ситуациях. В предлагаемой формулировке модели все параметры, которые должны быть определены для функций решения, испытывают такое воздействие величин уровней, которое приводит к установлению темпов потоков, предусмотренных решениями. Эти уровни в свою очередь корректируются ответными решениями. Неточный параметр функции решения может потребовать соответствующей корректировки уровней в модели, пока не будет достигнуто правильное соотношение темпов потоков. Приведем некоторые примеры для иллюстрации этой внутренней корректировки. При определении параметра, характеризующего запаздывание в погашении счетов дебиторов, можно избрать слишком большую величину; это приведет к тому, что уровень счетов дебиторов слегка возрастет, но темп погашения будет все же связан с тем темпом, в котором берутся новые обязательства. Принятие в модели слишком низкого уровня спроса покупателей на автомобили приведет к снижению их товарного запаса и к постепенному сокращению автомобильных перевозок до тех пор, пока уровень спроса на автомобили не повысится. Изменение в уровне запаса готовых автомобилей поможет уравновесить функцию решения неточного уровня покупок; при этом динамика изменения темпа покупок в количественном отношении останется правильной, если иметь в виду другие переменные величины модели.

Мы должны больше беспокоиться о том, что говорит модель относительно факторов, которые вызовут изменения в темпах и уровнях, чем о точности в определении средней величины темпов и уровней.

Если модель правильно сконструирована, то, как это ни удивительно на нее часто не. оказывают влияния изменения, которые могут иметь место в большинстве параметров — иногда даже изменения в каждом из них. Чувствительность к избранным величинам параметров в модели должна быть не больше, чем чувствительность реальной системы к соответствующим факторам. Представляется очёвидным, что наша действительная промышленно-экономическая активность не должна быть слишком чувствительной к основным параметрам этой активности и что эти параметры изменяются не быстро. Это должно быть так, потому что важнейшие характеристики наших организаций остаются неизменными в течение длительного времени. Процветающая фирма стремится остаться такой на длительный период. Успех ее основывается на ее структуре и политике (включая важнейшие аспекты руководства). Национальная экономика США продемонстрировала удивительно подобные повторяющиеся экономические циклы на протяжении своей истории, несмотря на значительные изменения в технологии, в структуре денежного обращения, в быстроте коммуникаций и транспортировки, в соотношении значения промышленности и сельского хозяйства и в активности правительства.

Нелинейные функции решения.Нелинейные модели упоминались в разделе 3.1. Нелинейность модели проявляется в функциях решений, регулирующих темпы потоков. Линейная зависимость — это такая зависимость, в которой вводимые факторы комбинируются путем простого сложения или вычитания для определения результата. Предположим, что темп R зависит от переменных факторов X, У и Z, как, например, в следующей линейной функции:

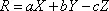
Здесь переменные X, Y и Z оказывают воздействие на R каждая в отдельности. В частности, переменные Y и Z не определяют влияния переменной X на результат R. Далее, любое влияние на R пропорционально соответствующей переменной ввода, независимо от абсолютной величины, которую она может иметь. Линейные решения недостаточны для описания тех зависимостей, с которыми нам приходится иметь здесь дело.