Джей Форрестер - Основы кибернетики предприятия

Имеются достаточные основания считать, что среди существующих реальных систем некоторые неустойчивы в обычном математическом понимании. Они не стремятся к состоянию статического равновесия (даже при отсутствии случайностей и внешнего возмущения). Они неустойчивы и обнаруживают стремление к увеличению амплитуды колебаний, которые поддерживаются непрерывными изменениями соотношения сил между нелинейными формами в системе. Наши социальные системы в высшей степени нелинейны и большую часть времени противодействуют ограничениям, связанным с недостатком рабочей силы и неприемлемой в политическом отношении безработицей, сокращением денежных ресурсов и преодолением инфляции, спадом деловой активности и недостатком средств производства. По-видимому, такие нелинейности в сочетании с тенденциями неустойчивости, порожденной усилениями и запаздываниями, создают характерный образ действий, который мы наблюдаем в экономических системах свободного предпринимательства.

Линейный анализ «малых сигналов» не пригоден для нелинейных неустойчивых систем. Такой анализ небольших нарушений равновесия по необходимости предполагает статическое равновесие и систему, которая стремится возвратиться к этому состоянию. Между тем результаты работы с динамическими моделями, а равно и наблюдаемое поведение реальных систем, приводят к заключению, что важные их проявления часто имеют нелинейный характер и относятся к типу «больших сигналов».

При построении модели, предполагающем устойчивость системы, из рассмотрения могут выпасть некоторые наиболее интересные и важные характеристики системы.

Базовая структура, состоящая ил переменных уровней и темпов потоков, отражает существо систем управления промышленным предприятием. Уровни определяют решения, которые управляют темпами потоков. Темпы потоков в свою очередь являются причиной изменений в уровнях. Уровни и темпы составляют шесть взаимосвязанных потоков, которые отражают деятельность промышленного предприятия. Пять из них — это потоки материалов, заказов, денежных средств, оборудования и рабочей силы. Шестой — информационный поток, является соединительной тканью пяти других потоков.

Теперь мы можем перейти к рассмотрению образца структуры модели, который соответствует задачам и принципам, изложенным в общих чертах в предыдущих главах. Для этого достаточно рассмотреть структуру простейшей модели. В частных случаях модель может стать сложной в силу своей величины и обилия деталей, но, как это будет показано в данной главе, основой ее по-прежнему останутся такие переменные, как «уровни» и «решения».

Форма модели должна позволить решать несколько задач. В связи с этим модель должна обладать следующими характерными чертами:

— иметь возможность отражать любую причинно-следственную связь, которую мы захотим учесть;

— иметь простую математическую форму;

— использовать терминологию, синонимичную языку общественных наук, экономики и производства;

— охватывать большое число переменных (тысячи), не превышая, однако, практических возможностей вычислительных машин, и

— быть пригодной для отражения «непрерывных» взаимодействий, с тем чтобы дискретные величины, вводимые в интервале времени между решениями, не оказывали влияния на результаты. Однако модель должна позволить произвести, если понадобится, дискретные изменения в решениях.

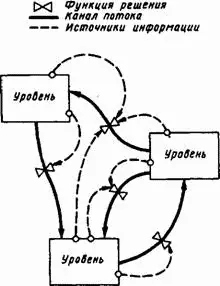
Указанным выше требованиям удовлетворяет динамическая структура, состоящая из резервуаров или уровней, связанных между собой управляемыми потоками, как показано на рис. 5–1.

Рис. 5–1 содержит четыре существенных элемента, которые ниже будут рассмотрены раздельно:

— несколько уровней;

— потоки, перемещающие содержимое одного уровня к другому;

— функции решений (изображенные в виде вентилей), которые регулируют темпы потока между уровнями;

— каналы информации, соединяющие функции решений с уровнями.

Эта базовая структура будет использована здесь даже применительно к промышленным и экономическим моделям, кажущимся на первый взгляд значительно более сложными. Если читатель получит ясное представление об этой структуре и о соответствующих ей основных уравнениях из последующей главы, он не встретит никаких трудностей при переходе и к более сложным моделям. В каждом отдельном случае более сложные системы будут, однако, состоять из четырех приведенных выше элементов основной структуры, показанной на рис. 5–1. В последующих параграфах будут рассмотрены все четыре элемента основной структуры модели.