Джей Форрестер - Основы кибернетики предприятия

DHR — 1,0 недели — минимальное запаздывание в розничном звене;

DHD = 1,0 недели — минимальное запаздывание в оптовой торговле;

DHF = 1,0 недели — минимальное запаздывание обработки заказа на заводе.

Необходимо также выбрать величины запаздываний выполнения заказов из-за отсутствия на складе необходимого товара DUR, DUD и DUF. При рассмотрении уравнения 13-6 мы на основе интуитивных предположений установим, что эти запаздывания пропорциональны отношению желательного запаса к фактическому. С помощью модели можно проверить влияние на систему выбора и других видов функциональной взаимосвязи и различных значений постоянной запаздывания, связанного с отсутствием на складе необходимого товара.

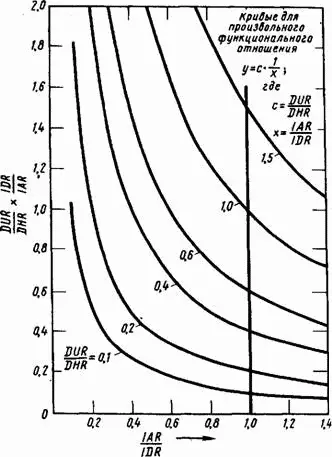
На рис. 13–17 показан ряд функций, из которых мы должны сделать выбор. По вертикальной оси отложена та часть общего среднего запаздывания, которая связана с отсутствием на складе необходимого товара; она выражена в долях минимального запаздывания DHR. По горизонтальной оси отложено безразмерное отношение фактического запаса к желательному. Отдельные кривые показывают различные отношения запаздывания DUR (связанного с отсутствием на складе некоторых товаров в то время, как их суммарное количество IAR находится на желательном уровне JDR) к запаздыванию DHR (минимальному времени, необходимому для оформления заказа).

На рис. 13–17 проведена жирная вертикальная линия в том месте, где фактический запас равен желательному. Точки, в которых кривые пересекают эту линию, соответствуют такому отношению запаздываний DUR и DHR, которое будет иметь место в условиях «нормальной» величины общего запаса. Приведенные кривые показывают, сколь быстро изменяется среднее запаздывание выполнения заказа при изменении запаса. Пока мы придерживаемся определенного функционального отношения, задаваемого уравнениями 13-6, 13–24 и 13–42, мы не можем независимо выбирать величину запаздывания DUR при нормальном запасе товаров и скорость, с какой будет увеличиваться это запаздывание, при сокращении наличия товаров. Желательное соотношение между этими величинами можно установить, принимая различные функциональные отношения между запасом и запаздыванием [80]. Допустим, что кривые, обозначенные 0,4; 0,6 и 1,0, согласуются соответственно с нашей оценкой запаздываний выполнения заказов розничной и оптовой торговлей и производством из-за отсутствия на складах необходимых товаров. Для определения абсолютных величин этих запаздываний приведенные в обозначениях числа надо умножить на минимальное запаздывание, которое уже выбрано нами равным 1 неделе; поэтому запаздывания для розничной и оптовой торговли и производства будут равны соответственно:

DUR = 0,4 недели,

DUD — 0,6 недели,

DUF = 1,0 недели.

Принятие таких значений отношения запаздываний DUR и DHR означает, например, что, если запас товаров в рознице сократится до половины желательного количества, то среднее запаздывание выполнения заказа розничным звеном увеличится с 1,4 до 1,8 минимального времени, необходимого для выполнения заказа. В оптовой торговле соответствующее запаздывание увеличилось бы с 1,6 до 2,2 раза по сравнению с минимальным, а в производстве — с 2 до 3 раз. Оценка достоверности этих значений в конкретной ситуации могла бы быть произведена на основе анализа движения типичных заказов с целью определить характерное для них время выполнения и величину запаздывания из-за отсутствия на складе некоторых товаров.

Следующую группу составляют параметры, которые связывают уровень желательного запаса товаров со средним темпом продаж. Эти константы определяются числом недель, в течение которых средний темп продаж может быть обеспечен за счет «нормального» запаса товаров.

Пусть эти константы для розничной и оптовой торговли и производства будут равны соответственно:

AIR = 8 неделям,

AID = 6 неделям,

AIF = 4 неделям.

Если мы разделим эти константы на 52 недели, то получим темп оборачиваемости запаса товаров в течение года. Приведенные выше цифры соответствуют оборачиваемости запасов в трех подразделениях системы, соответственно 6,5; 8,7 и 13 раз в год.

Параметры в уравнениях 13-8, 13–26 и 13–44 дают показательную постоянную времени усреднения, которая используется при определении усредненного темпа продаж на основе текущих значений этого темпа. Мы допустим в начале нашего исследования, что для каждого из трех подразделений эта константа равна 8 неделям: