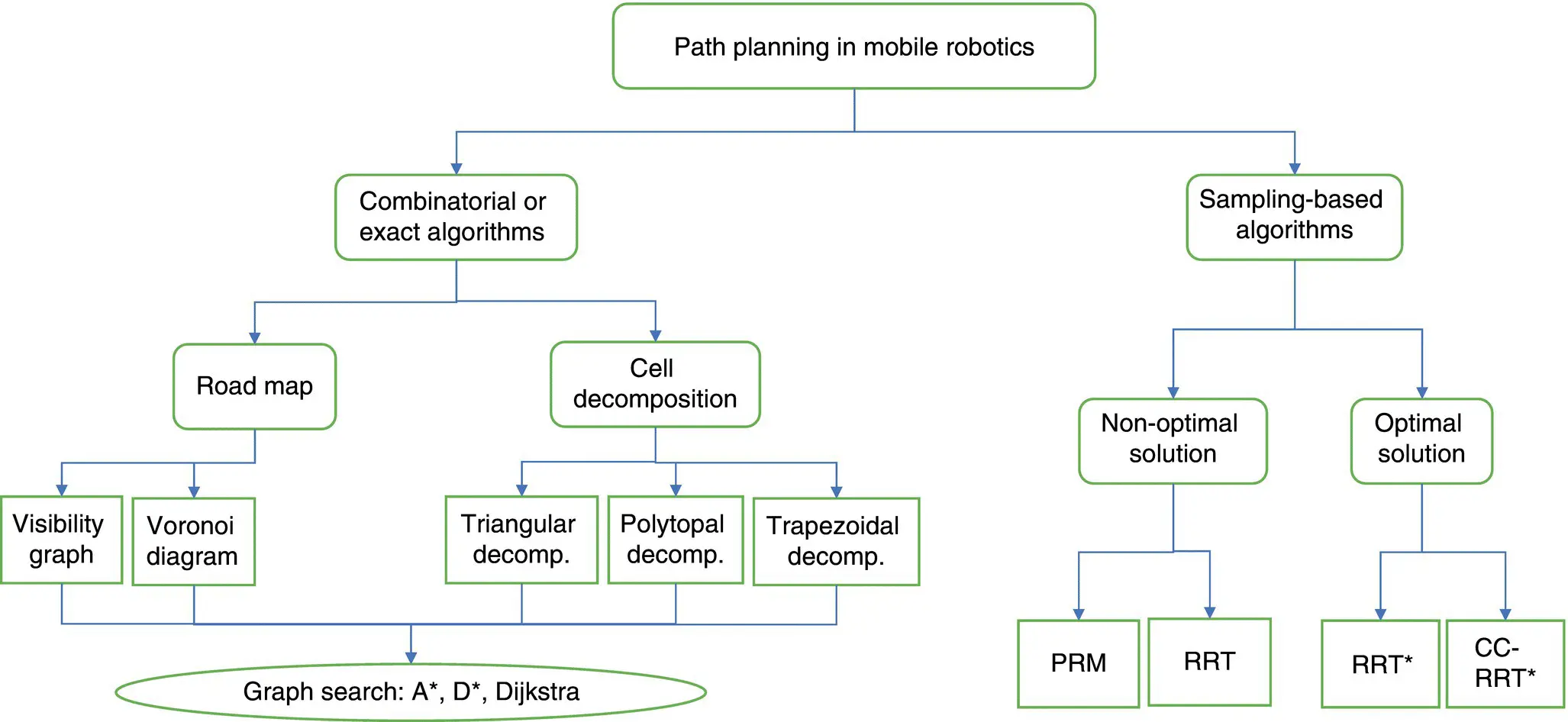
Figure 1.4 Path planning methods. Main categories for path planning in mobile robotics and examples of some well‐known methods for each of them.
The second big category comprising exact planning algorithms is cell decomposition. This strategy is based on partitioning the free configuration space into a finite set of regions that can be safely traversed by a robot. Cell decompositions are often employed in high‐level planning approaches where the robot may visit some regions based on logic or temporal requirements (this feature is extended in Section 1.4and in subsequent chapters).
It bears mentioning that the exact methods further need graph search algorithms in order to finally obtain the optimal route connecting a series of waypoints. For this aspect, three graph search algorithms that return a minimum cost path are usually employed, namely Dijkstra [53], A* [140, 160, 221], and D* [195]. Dijkstra and A* algorithms are great choices for static graphs with positive known arc weights, with A* additionally requiring a heuristic cost function. The D* algorithm, proposed by Anthony Stentz in 1995 [195], constitutes an extension of the classic A* algorithm for graphs, introduced by Nils J. Nilsson in the 1970s [160]. D* considers the 2D map as a cost map where each weight represents the cost of traversing each cell in the horizontal or vertical direction. For cells corresponding to obstacles we can give a huge cost, so D* finds the path minimizing the total cost of travel. This cost may deal with various aspects such as time to drive across a cell, roughness of the terrain, etc. The key feature of D* is that it supports incremental replanning, that is, the algorithm can replan the initial route while the robot discovers that the world is different from the initial plan. The incremental replanning has a lower computational cost than completely replanning, as would be required by A* [41]. The algorithm D* accounts for many successful applications in mobile robotics. For example, in [84], the D* algorithm is used for generating the optimal route for ground autonomous vehicles. More specifically, the cost function associated with the D* algorithm is configured in such a way that the route connecting two points minimizes the uncertainty associated with the elevation of the 3D points in the maps. This route also avoids points where the robot may experience a high risk of entrapment. After the successful introduction of the D* algorithm, there is a recent and broad body of research dealing with extending the features of this algorithm. Some of those recent algorithms are: D* Lite [125], PHI* [57], and E* [169].
Together with combinatorial or exact planning algorithms, another broad body of research in the field of path planning nowadays is related to sampling‐based planning methods. The first algorithm, called Probabilistic Roadmap (PRM), was proposed by Lydia E. Kavraki and Jean‐Claude Latombe in the 1990s [106]. The advantage of PRM is that relatively few points need to be tested to ascertain that the points and the paths between them are obstacle free [41]. The efficacy of several variations of the PRM algorithm is discussed in [75].
A major drawback of PRM is that it assumes that the robot is a point with omnidirectional capabilities. The Rapidly exploring Random Tree (RRT) algorithm takes into account the model of the robot, e.g. differential‐drive motion [134]. However, the main drawback of RRT is that it does not lead to an optimal path. This aspect is overcome by a variant of RRT called RRT*; this algorithm does guarantee the optimality and can find the optimal trajectory when applied to complex non‐holonomic systems [2, 104, 138]. In recent literature, there are numerous RRT‐based strategies trying to ensure optimality despite uncertainty in the motion of the robot [136, 143].
1.3 Motion control. Definition and historical background
The key goal of a mobile robot is to follow the route generated by the path planner, and this goal is responsible for the motion controller. More specifically, robot control deals with the problem of determining the forces (or velocities) that must be developed by the robotic actuators in order for the robot to go to a desired position, track a desired trajectory, and, in general, perform some tasks with desired performance requirements [202].
The control problem can be classified depending on how the reference path is defined: a single target point  , a set of waypoints
, a set of waypoints 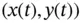 , or a set of poses
, or a set of poses 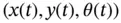 , where
, where  is the time. The time in the previous variables represents a situation where those variables may change along the robot operation. In this sense, the control strategy can be understood as the problem of moving to a point, path following, and trajectory tracking, see Figure 1.5. Notice that, in the trajectory tracking problem the robot orientation must also be controlled, unlike in the other two cases where the final robot orientation depends on the starting position.
is the time. The time in the previous variables represents a situation where those variables may change along the robot operation. In this sense, the control strategy can be understood as the problem of moving to a point, path following, and trajectory tracking, see Figure 1.5. Notice that, in the trajectory tracking problem the robot orientation must also be controlled, unlike in the other two cases where the final robot orientation depends on the starting position.
Essentially the control problem must ensure
(1.1) 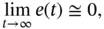
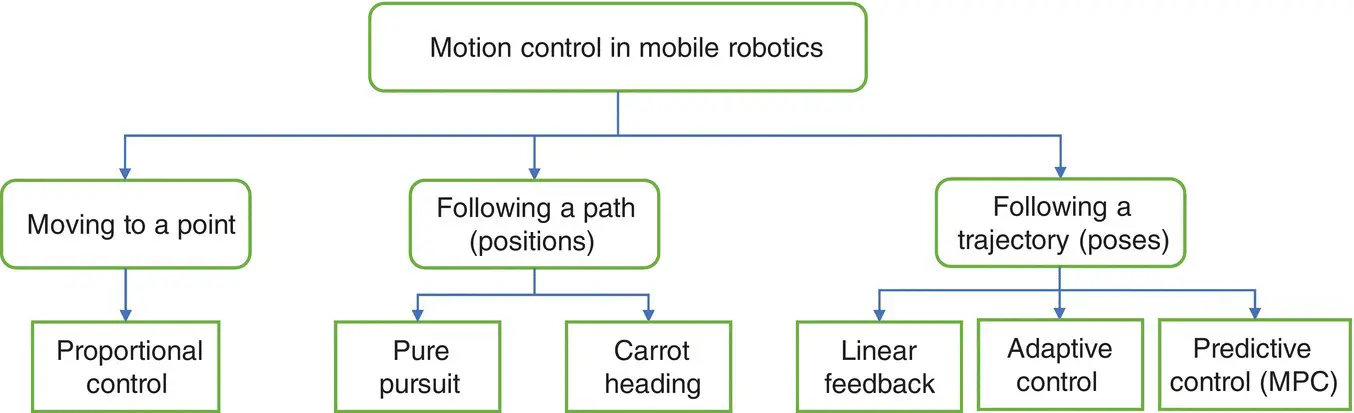
Figure 1.5 Motion control methods. Main categories for motion control in mobile robotics and an example of some well‐known methods for each of them.
where 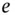 is the error between the actual position of the robot and the desired target position. Notice that Eq. (1.1)defines a quasi‐zero error because in some situations, for instance considering uncertainty, an exact error equal to zero cannot be achieved [81]. The control problem associated with a mobile robot can then be defined as a feedback control system. The idea is that the controller senses the position/pose of the robot, compares it against the desired reference, computes corrective actions based on a model of the robot and actuates the robot to effect the desired change. As highlighted in [9], the key issues in designing control logic are ensuring that the dynamics of the closed‐loop system are stable (bounded disturbances give bounded errors) and that they have additional desired behavior (good disturbance attenuation and fast responsiveness to changes in the operating point, among others).
is the error between the actual position of the robot and the desired target position. Notice that Eq. (1.1)defines a quasi‐zero error because in some situations, for instance considering uncertainty, an exact error equal to zero cannot be achieved [81]. The control problem associated with a mobile robot can then be defined as a feedback control system. The idea is that the controller senses the position/pose of the robot, compares it against the desired reference, computes corrective actions based on a model of the robot and actuates the robot to effect the desired change. As highlighted in [9], the key issues in designing control logic are ensuring that the dynamics of the closed‐loop system are stable (bounded disturbances give bounded errors) and that they have additional desired behavior (good disturbance attenuation and fast responsiveness to changes in the operating point, among others).
It is important to remark that mobile robotics comprises a challenging field from a control standpoint as there are some phenomena that influence robot's controllability, such as hard constraints fulfillment (e.g. physical limitations of actuators, narrow workspaces), and uncertainties (e.g. unmodelled dynamics, simplified models, noisy measurements). For that reason, in the past few years, many research efforts have been devoted to the application of different control strategies.
Читать дальше


 , a set of waypoints
, a set of waypoints 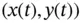 , or a set of poses
, or a set of poses 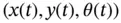 , where
, where  is the time. The time in the previous variables represents a situation where those variables may change along the robot operation. In this sense, the control strategy can be understood as the problem of moving to a point, path following, and trajectory tracking, see Figure 1.5. Notice that, in the trajectory tracking problem the robot orientation must also be controlled, unlike in the other two cases where the final robot orientation depends on the starting position.
is the time. The time in the previous variables represents a situation where those variables may change along the robot operation. In this sense, the control strategy can be understood as the problem of moving to a point, path following, and trajectory tracking, see Figure 1.5. Notice that, in the trajectory tracking problem the robot orientation must also be controlled, unlike in the other two cases where the final robot orientation depends on the starting position.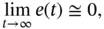

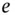 is the error between the actual position of the robot and the desired target position. Notice that Eq. (1.1)defines a quasi‐zero error because in some situations, for instance considering uncertainty, an exact error equal to zero cannot be achieved [81]. The control problem associated with a mobile robot can then be defined as a feedback control system. The idea is that the controller senses the position/pose of the robot, compares it against the desired reference, computes corrective actions based on a model of the robot and actuates the robot to effect the desired change. As highlighted in [9], the key issues in designing control logic are ensuring that the dynamics of the closed‐loop system are stable (bounded disturbances give bounded errors) and that they have additional desired behavior (good disturbance attenuation and fast responsiveness to changes in the operating point, among others).
is the error between the actual position of the robot and the desired target position. Notice that Eq. (1.1)defines a quasi‐zero error because in some situations, for instance considering uncertainty, an exact error equal to zero cannot be achieved [81]. The control problem associated with a mobile robot can then be defined as a feedback control system. The idea is that the controller senses the position/pose of the robot, compares it against the desired reference, computes corrective actions based on a model of the robot and actuates the robot to effect the desired change. As highlighted in [9], the key issues in designing control logic are ensuring that the dynamics of the closed‐loop system are stable (bounded disturbances give bounded errors) and that they have additional desired behavior (good disturbance attenuation and fast responsiveness to changes in the operating point, among others).