Marcus du Sautoy - What We Cannot Know

But a discovery at the end of the twentieth century even questions Laplace’s basic tenet of the theoretical predictability of the future. In the early 1990s a PhD student by the name of Zhihong Xia proved that there is a way to configure five planets such that when you let them go, the combined gravitational pull causes one of the planets to fly off and reach an infinite speed in a finite amount of time. No planets collide, but still the equations have built into them this catastrophic outcome for the residents of the unlucky planet. The equations are unable to make any prediction of what happens beyond this point in time.

Xia’s discovery is a fundamental challenge to Laplace’s view that Newton’s equations imply that we can know the future if we have complete knowledge of the present, because there is no prediction even within Newton’s equations for what happens next for that unlucky planet once it hits infinite speed. The theory hits a singularity at this point, beyond which prediction makes no sense. As we shall see in later Edges, considerations of relativity will limit the physical realization of this singularity since the unlucky planet will eventually hit the cosmic speed limit of the speed of light, at which point Newton’s theory is revealed to be an approximation of reality. But it nevertheless reveals that equations aren’t enough to know the future.

It is striking to listen to Laplace on his deathbed. As he sees his own singularity heading towards him with only a finite amount of time to go, he too admits: ‘What we know is little, and what we are ignorant of is immense.’ The twentieth century revealed that, even if we know a lot, our ignorance will remain immense.

But it turns out that it is isn’t just the outward behaviour of planets and dice that is unknowable. Probing deep inside my casino dice reveals another challenge to Laplace’s belief in a clockwork deterministic universe. When scientists started to look inside the dice to understand what it is made of, they discovered that knowing the position and the movement of the particles that make up the dice may not even be theoretically possible. As I shall discover in the next two Edges, there might indeed be a game of dice at work that controls the behaviour of the very particles that make up my red Las Vegas cube.

Everyone takes the limits of his own vision for the limits of the world.

Arthur Schopenhauer

When I started at my comprehensive school, I remember my music teacher asking the class if there was anyone who wanted to learn a musical instrument. Three of us put up our hands. The teacher led us into the storeroom cupboard to see what instruments were available. The cupboard was bare except for three trumpets stacked up on top of each other.

‘It looks like you’re learning the trumpet.’

I don’t regret the choice (even if there wasn’t one). I had a great time playing in the local town band and larking around in the brass section of the county orchestra as we counted bars rest. But I used to look over with a little envy at the strings who seemed to be playing all the time, getting all the good tunes. A few years ago, during a radio interview, I was asked what new musical instrument I would choose to learn, given the opportunity, and which piece of music I would aspire to play.

‘The cello. Bach’s suites.’

The question has been nagging at the back of my mind since that interview: could I learn to play those beautiful cello suites? Perhaps it was too late to pick up such new skills, but I needed to know. So I bought a cello.

It sits behind me as I write about trying to predict the outcome of the dice. When I need a break from analysing the equations that control the fall of the red cube on my desk, I massacre one of the gigues from the first suite for cello. I can feel Bach turning in his grave but I am enjoying myself.

One of the fun things about the cello is the possibility of sliding your finger up the string to create a continuous glissando of notes. Not something I can do on my trumpet, which is an instrument of discrete notes corresponding to the different combinations of fingers I put down. It turns out that this tension between the continuous glissando of the cello and the discrete notes of the trumpet is relevant to my attempts to predict the behaviour of my dice.

To predict how the dice might land I need to know what my cube is made from. Denser acetate in one corner of the shape will lead to one side of the dice being favoured over the others. So if I am going to attempt to apply Newton’s laws to my dice as it tumbles through the air, I need to know how my dice is put together. Is it a continuous structure, or, if I look closely, is it made up of discrete pieces?

If I accept the limits of my own vision, as Schopenhauer’s quote at the beginning of this Edge suggests I tend to, then I can’t see anything other than the clear red acetate that makes up the dice. But with an optical microscope I can magnify the dice by a factor of 1500, which would scale my dice up to the size of a large building. Peering inside this huge dice still won’t reveal much about the secrets of how it is built. Everything still looks pretty smooth and continuous.

In the twentieth century microscopes exploiting different bits of the electromagnetic spectrum have allowed scientists to create images which magnify things a further 1000 times. Now my dice will span from one side of London to the other. At this magnification the dice is looking grainier. The sense of the continuous structure is giving way to something more discrete. Current electron microscopes allow me to zoom in another 10 times closer, at which point I might start to see the carbon and oxygen atoms that I know are some of the ingredients of the acetate from which my dice is made.

The intriguing thing is that scientists had already formulated an atomic view of matter long before I could actually see these atoms under the modern microscopes in the labs across the road from the mathematics department. And it is a combination of a mathematical and theoretical perspective with a physical vision that is the best tool for knowing what my dice is made from.

But atoms like oxygen and carbon turned out not to be as atomic as the name suggests. Beyond the atomic structure revealed by current electron microscopes, I know that there is more internal structure. Atoms give way to electrons, protons and neutrons. Protons and neutrons in turn give way to quarks. In 2013 quantum microscopes even captured pictures of electrons orbiting the nucleus of a hydrogen atom. But is there a theoretical limit to how far I can dig down inside my dice?

What happens, for example, if I take my dice and keep dividing it in half? Just how far can I go? The mathematical side of me says: no problem. If I have a number I can keep dividing it by two:

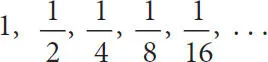
There is no point mathematically where I have to stop. Yet if I start trying to do the same thing with the physical dice sitting on my desk and cut it in half, then in half again, just how far can I keep going?