Marcus du Sautoy - What We Cannot Know

From that moment on the name of Henri Poincaré became known to the public, who then became accustomed to regarding our colleague no longer as a mathematician of particular promise but as a great scholar of whom France has the right to be proud.

Preparations began to publish Poincaré’s solution in a special edition of the Royal Swedish Academy of Science’s journal Acta Mathematica . Then came the moment every mathematician dreads. Every mathematician’s worst nightmare. Poincaré thought his work was safe. He’d checked every step in the proof. Just before publication, one of the editors of the journal raised a question over one of the steps in his mathematical argument.

Poincaré had assumed that a small change in the positions of the planets, a little rounding up or down here or there, was acceptable as it would result in only a small change in their predicted orbits. It seemed a fair assumption. But there was no justification given for why this would be so. And in a mathematical proof, every step, every assumption, must be backed up by rigorous mathematical logic.

The editor wrote to Poincaré for some clarification on this gap in the proof. But as Poincaré tried to justify this step, he realized he’d made a serious mistake. He wrote to Gösta Mittag-Leffler, the head of the prize committee, hoping to limit the damage to his reputation:

The consequences of this error are more serious than I first thought. I will not conceal from you the distress this discovery has caused me … I do not know if you will still think that the results which remain deserve the great reward you have given them. (In any case, I can do no more than to confess my confusion to a friend as loyal as you.) I will write to you at length when I can see things more clearly.

Mittag-Leffler decided he needed to inform the other judges:

Poincaré’s memoir is of such a rare depth and power of invention, it will certainly open up a new scientific era from the point of view of analysis and its consequences for astronomy. But greatly extended explanations will be necessary and at the moment I am asking the distinguished author to enlighten me on several important points.

As Poincaré struggled away he soon saw that he was simply mistaken. Even a small change in the initial conditions could result in wildly different orbits. He couldn’t make the approximation that he’d proposed. His assumption was wrong.

Poincaré telegraphed Mittag-Leffler to break the bad news and tried to stop the paper from being printed. Embarrassed, he wrote:

It may happen that small differences in the initial conditions produce very great ones in the final phenomena. A small error in the former will produce an enormous error in the latter. Prediction becomes impossible.

Mittag-Leffler was ‘extremely perplexed’ to hear the news.

It is not that I doubt that your memoir will be in any case regarded as a work of genius by the majority of geometers and that it will be the departure point for all future efforts in celestial mechanics. Don’t therefore think that I regret the prize … But here is the worst of it. Your letter arrived too late and the memoir has already been distributed.

Mittag-Leffler’s reputation was on the line for not having picked up the error before they’d publicly awarded Poincaré the prize. This was not the way to celebrate his monarch’s birthday! ‘Please don’t say a word of this lamentable story to anyone. I’ll give you all the details tomorrow.’

The next few weeks were spent trying to retrieve the printed copies without raising suspicion. Mittag-Leffler suggested that Poincaré should pay for the printing of the original version. Poincaré, who was mortified, agreed, even though the bill came to over 3500 crowns, 1000 crowns more than the prize he’d originally won.

In an attempt to rectify the situation, Poincaré set about trying to sort out his mistake, to understand where and why he had gone wrong. In 1890, Poincaré wrote a second, extended paper explaining his belief that very small changes could cause an apparently stable system suddenly to fly apart.

What Poincaré discovered, thanks to his error, led to one of the most important mathematical concepts of the last century: chaos. It was a discovery that places huge limits on what we humans can know. I may have written down all the equations for my dice, but what if my dice behaves like the planets in the solar system? According to Poincaré’s discovery, if I make just one small error in recording the starting location of the dice, that error could expand into a large difference in the outcome of the dice by the time it comes to rest on the table. So is the future of my Vegas dice shrouded behind the mathematics of chaos?

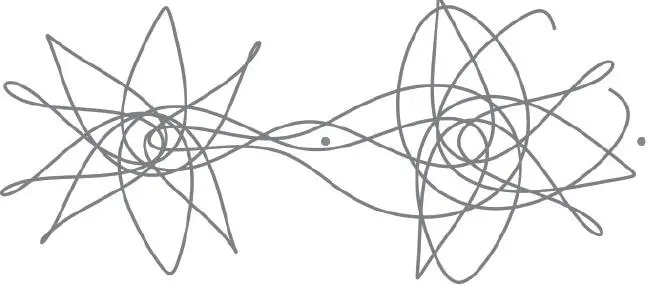
The chaotic path mapped out by a single planet orbiting two suns.

If nature were not beautiful it would not be worth knowing, and if nature were not worth knowing, life would not be worth living.

Henri Poincaré

I wasted a lot of time at university playing billiards in our student common room. I could have pretended that it was all part of my research into angles and stuff, but the truth is that I was procrastinating. It was a good way of putting off having to cope with not being able to answer that week’s set of problems. But in fact the billiard table hides a lot of interesting mathematics in its contours. Mathematics that is highly relevant to my desire to understand my dice.

If I shoot a ball round a billiard table and mark its path, then follow that by shooting another ball off in very nearly the same direction, the second ball will trace out a very similar path to the first ball. Poincaré had believed that the same principle applied to the solar system. Fire a planet off in a slightly different direction then the solar system will evolve in a very similar pattern. This is most people’s intuition: if I make a small change in the initial conditions of the planet’s trajectory it won’t alter the course of the planet much. But the solar system seems to be playing a slightly more interesting game of billiards than the one I played as a student.

Rather surprisingly, if I change the shape of the billiard table this intuition turns out to be wrong. For example, fire balls round a billiard table shaped like a stadium with semicircular ends but straight sides and the paths can diverge dramatically even though they started in almost the same direction. This is the signature of chaos: sensitivity to very small changes in the initial conditions.

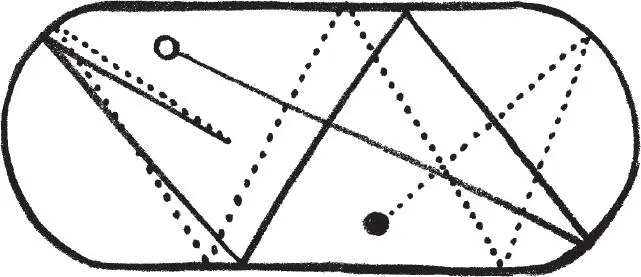
Two quickly diverging paths taken by a billiard ball round a stadium-shaped billiard table.

So the challenge for me is to determine whether the fall of my dice is predictable, like a conventional game of billiards, or whether the dice is playing a game of chaotic billiards.

Despite Poincaré being credited as the father of chaos, it is striking that this sensitivity of many dynamical systems to small changes was not very well known for decades into the twentieth century. Indeed, it really took the rediscovery of the phenomenon by scientist Edward Lorenz, when he, like Poincaré, thought he’d made some mistake, before the ideas of chaos became more widely known.