Robert G. Reynolds - Cultural Algorithms

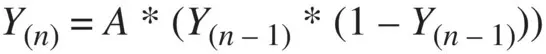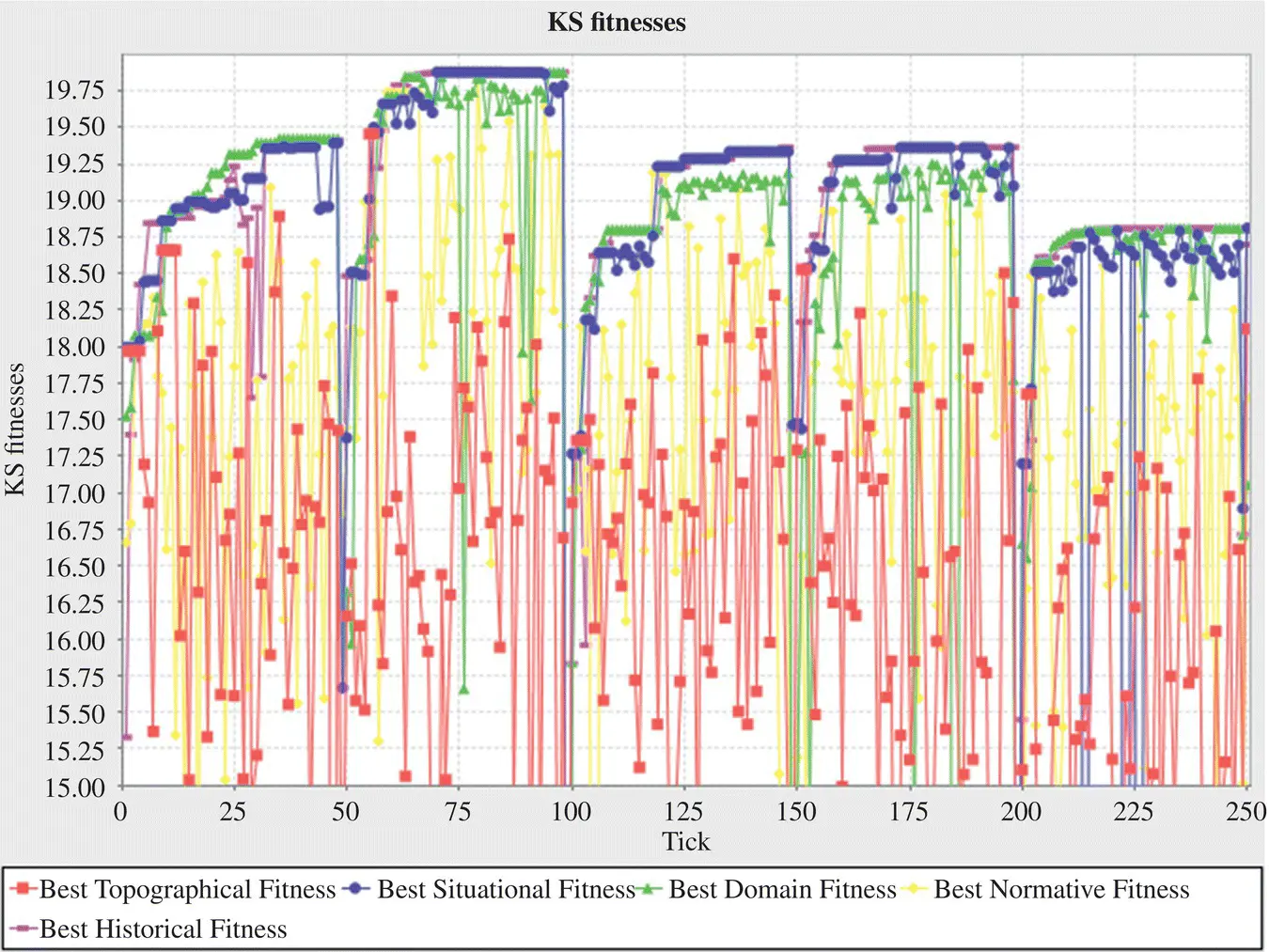
Figure 2.6 ConesWorld KS Fitness with a regular topographical update at every 50 ticks, with variable cone heights.

The logistics function ( Figure 2.7) utilized by the CAT System, notably in the update mechanism for the topographic of the ConesWorld fitness function, is a recursive function that generates a value between 0 and 1. This value is then used by the update mechanism to select a fractional amount of the allowable rate of change that the system specifies.

Given an A value between 0 and 4, successive iterations of the logistics function will generate a fluctuation between the values of 0 and 1. The frequency of this fluctuation is dependent on the size of the A value. Due to the recursive nature of the function, low values of A will result in subsequent values of Y (n)approaching a steady output that will cease to fluctuate after a sufficient number of iterations. For this reason, using lower values of A in the ConesWorld simulation will result in the appearance of smooth, predictable, near‐linear transitions from one update to the next.

However, as the A value approaches 3, the resulting fluctuations becomes more self‐sufficient and will maintain a steady, regular frequency between two absolutes, which its peaks and valleys will trend toward. For these cases, it is possible to have subsequent steps of the logistics function vary, but in predictable ways. As each cone in the ConesWorld simulation freshly calculates the logistics function with the next iteration of Y (n), alternating cones querying it for their rate of change will receive alternating high and low rates from it.

After exceeding an A value of 3.33, the logistics function enters into a self‐sufficient, non‐maintaining erratic frequency with relatively unpredictable shifts in frequency, without ever stabilizing to a constant, repetitive cycle. As seen in Figure 2.8, the lower values of A , ranging from 0 to 3 in the forefront, quickly reduce to a singular output after a brief initial period. After A reaches 3, the frequency does not reduce, but rather becomes a self‐perpetuating frequency that continues indefinitely without diminishing.

In those rows of the graph beyond 3.33, the pattern becomes erratic, with each subsequent iteration of the logistics function taking a dramatic, seemingly unpredictable movement that bears little relation to the patterns produced by lower values of A . It should also be noted that even with this erratic fluctuation the resulting Y (n)values are still within the range of 0 and 1. However, should the A value exceed 4, then the system will destabilize and quickly break out of the given range.

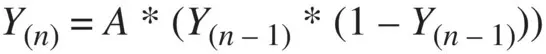
Figure 2.7 The CAT System Logistics Function.

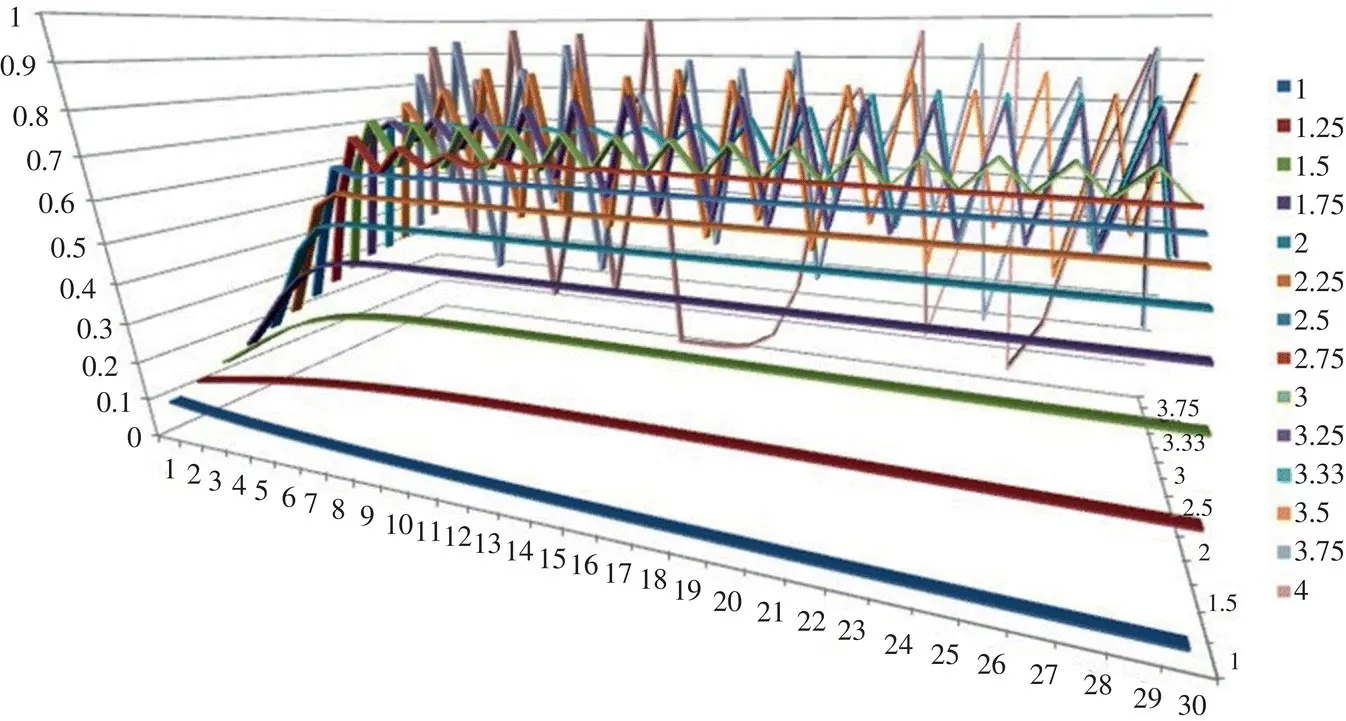
Figure 2.8 A three‐dimensional visualization of successive iterations of the logistics function across increasing values of A .

The following data are the result of two separate runs of the CAT system's ConesWorld simulation. Both runs use similar parameters for their initializations. The population consists of 50 agents in each of them; the social topology between them is represented by lBest (each agent having a connection to 2 agents, resulting in a circular chain); the influence is calculated by Majority; the number of cones is 150 (it must be noted that some smaller cones can be consumed by larger cones and not be visible during the simulation); and the A ‐values for height, radius, and position are all 3.5

The difference between the two runs is the usage of the system's dynamic landscape. For the first run, the landscape remains static across 20 generations. For the second run, the landscape dynamically updates every 5 generations, for 4 separate landscapes. This combination results in both simulations running for 20 generations, with the second run using (5 generations * 4 landscapes) for its 20. The agents present in each run are persistent in their respective runs, meaning that those agents in the static landscape carry the continuous knowledge of the landscape from initialization until the system stops on the twentieth generation. Similarly, those agents in the dynamic landscape are also persistent, so even though the landscape changes every 5 generations, they continue to possess their past knowledge of the landscape.

The initialization step of each run occurs when the system takes the data used to establish the parameters of the simulation, and generates the given number of cones. While the number of cones is set at 150, a number of these cones are not readily visible, as they are absorbed by the larger cones. Whenever two or more cones overlap, the system is designed to take the maximum of those cones at the given points where they overlap. Those cones subsumed by larger cones in the static landscape will remain hidden throughout the entirety of the run, while those hidden cones in the dynamic landscape have a chance of becoming visible when the dynamic landscape is updated and the dimensions of the cones are altered.

The A ‐values fed into the logistics function are used to determine the relative dimensions of each cone. For a given acceptable range of values for the cones to have, each cone will be individually defined based on repeated initial calls of the logistics function as a means of seeding the function, followed by subsequent calls to the function for each newly generated cone. This means that a low A value, which results in the linear results seen in The Cones World section, used for initialization will result in a number of cones that are not terribly dissimilar from one another, the changes in their dimensions being gradual and slight. Using a higher A value, such as 3.5 which was used in these two runs, will result in subsequent calls to the logistics function returning a more chaotic frequency. For this reason, subsequently generated cones can differ dramatically from one another.

A point of interest in Figure 2.9is the distribution of agents at the time of initialization. They are homogeneously distributed across the landscape, evenly spaced out from one another as well as along the borders of the landscape. With the lBest social network topology visualized, they can be seen connected to one another by a zig‐zagging line and each agent connected to two neighbors. For the purposes of finding a maximum, the early configuration provides a unique sampling of early information for each of the knowledge sources to use. It is for this reason that later we may observe that, once the agents begin to cluster around likely candidates, the dynamic updates can result in a slower ascent back to the maximum. This is because the agents are now tightly clustered and thus yield less relevant data back to their respective knowledge sources.

When viewing the network connections across successive steps, it is possible to see the agents begin to concentrate on a maximum via the convergence of lines. In Figure 2.10, the first two steps depicted on the static landscape on the left indicate that some of the agents have located a local maximum and are investigating it. But as more information is gathered, notice that the large cone towards the right side of the static landscape is abandoned by step 3, as the agents converge more on the overall maximum that has been located. The network takes a denser appearance as more agents gather, and other agents are sent out to explore with the majority remaining with the highest scoring locations.