Microgrid Technologies

To solve a problem in micro-grid, the MSE follows some steps:

1 a. Prediction of uncertain parameters

2 b. Uncertainty modeling

3 c. Mathematical formulation

4 d. Optimization

Uncertainty is the possibility of deference in real and forecasted values due to a lack of information [34]. This uncertainty in MG may be in operational parameters or in economic parameters. The operational parameters include the quantity of power generated and the quantity of power consumption. On the other hand, the economic parameter includes the effects on economic aspects such as production cost, financial growth and rate of interest, etc. [35].

The uncertain parameters can be predicted in various time ranges that are of the very small time period, a few minutes to a couple of days, which is called prediction of short term. In the prediction of mid-term, the time range is from several weeks to a few months. And in the prediction of the long term, it ranges from few months to several years [36]. The MG problems are considered for hourly intervals, so short term prediction is the best method for this.

The MSE faces difficulty during decision making because of the uncertainty. That is why a verity of ways have been implemented to manage the uncertainty. Those methods are called uncertainty modeling [35]. There are some methods like stochastic method, ANN method, fuzzy method, robust optimization method and information gap decision theory [37–39].

The management of energy in a microgrid can be formulated mathematically as a problem of optimization with the primary aim to schedule the functionality of DGs, SSEs and loads for the short term with specific objective functions and the constraints of the components of MG. The capital cost and the operational cost are taken as the objective functions. Fuel cost, maintenance cost, start-up and short-down losses and degradation are considered as the operational cost. There are different constraints which can affect an MSE. Some cases maximum and minimum limit of the generation unit affects their safety and economic performance. The source and load balance are also a constraint that has to be taken. The rate of charging and rate of discharging of energy storage body can also be taken as a constraint. The bus voltage, feeder current, frequency, etc. are some technical constraints [40, 41].

In the literature, there are many optimization techniques used for MSE in MGs [26]. Some examples are like (i) Heuristic approach (ii) MAS (iii) CPLEX solver (iv) SNOPT solver, etc.

In Ref. [42] the authors have studied the micro-grid consisting of several renewable energy sources with EMS. They have taken the goal function as the cost minimization of energy, which is the net cost of RES per annual cost of the net energy produced. Now the optimization objective is subjected to various constraints, such as reliability, economic conditions and environmental conditions. The criteria of reliability can be considered as the amount of energy cannot be supplied when the amount of power demand is more than the power generation. In economic condition, all of the cost includes installation cost, running cost. The environmental constraint is about the amount of CO2 emitted related to distributed generation system.Multi-objective optimization has been implemented by the authors of Ref. [43]. They have done the optimization for keeping power balanced in-between generation and utilisation, taking more than one objective functions. The objective functions can be taken, such as bus voltage stability, maximum power extraction from PV panel, maximum battery protection by keeping it in a suitable range of SOC. Reduction in hydrogen consumption minimized the fluctuation.

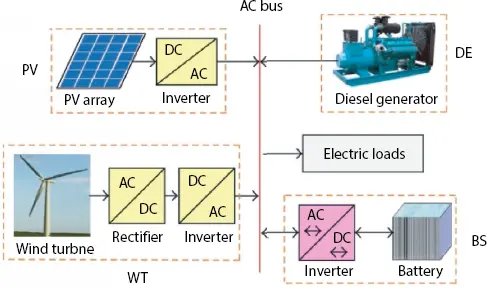
Figure 1.6 Micro-grid in Islanded mode.

The authors of Ref. [44] have expressed an MSE for the microgrid in standalone style such as solar power or wind power, etc. which has an objective function of cost reduction. The cost of an MG is consisting of the cost of energy injected by the distributed sources, the cost of energy storage unit like the cost of energy during charging or discharging, expenditure on the utilized energy, and the charges of penalty for undelivered power.

In Ref. [14], the authors have developed an MSE for different distributed sources like wind turbine ‘WT’, photovoltaic ‘PV’, plug-in EV ‘PEV’, diesel generator system ‘DGS’ and battery in islanded microgrid. The objective function is to make the best use of the number of adjustable loads during the islanded operation manner. The problem of optimization has been utilised to balance power. The constraints are load, limitation of the power generator and also battery specification.

In Ref. [45], the researchers have specified an idea about a cost-effective structure of thermal power plant. The goal of optimization is to decrease the cost of fuel of the thermal generators, taking consideration of the effect of the loading at the valve’s point. The constraints are power balancing, power generator’s limitations, and the ranges of operation of prohibited generators and its limits of ramp rate.

In Ref. [6], the authors have represented a cost minimization EMS of GC–HKT system with a storage system, which consists mainly of three types of costs. The energy purchasing cost from the grid satisfies the load requirement and also the battery charging is the initial cost. The second cost is during the high costing time the revenue comes from exporting electricity to the primary grid. The third one is wearing cost or maintenance cost in the system. The authors choose power balance, limitations of HKT’s production and SOC of the battery as optimization constraints.

The authors in Ref. [46] have optimized GC MG with generators, Energy Storage System and electrical load. The generators maybe detachable or not. The overall energy charges are assumed as the goal function. Such as the fuel utilization cost, cost of charging the battery, cost of discharging the battery, the energy cost generated by detachable and non-detachable generators, the energy cost generated by trading power in between MG and the main grid network, and the cost of conveying energy demand all over the arrangement. The authors have incorporated environmental and technological factors as constraints to get the optimized result. The total quantity of energy produced by the end of the generator should be the same as the total quantity of energy at the consumption. The consumer and supplier of electricity are taken as technical constraints. Energy storage constraints include charging/discharging limitations of battery, the energy balance of battery, energy storage limitations and SOC of battery. In the end, the constraint was grid limitations that the quantity of exchanged energy in between the main grid network and MG.

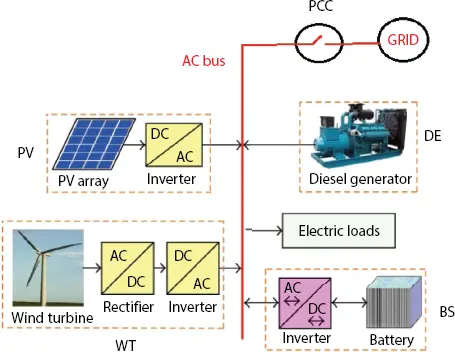
Figure 1.7 Microgrid in Grid Connected mode.