Space Physics and Aeronomy, Solar Physics and Solar Wind

It is possible that both phenomena, that is, a mixture of quasi‐linear waves and coherent structures, coexist within the kinetic range of scales. This can be at the origin of a balance between linear and nonlinear effects (the so‐called critical balance ). To verify this point, one needs to find a way to estimate characteristic times at different scales of the kinetic range.

Particle distributions in interplanetary space have been studied over many decades with Helios , Ulysses , Wind , Cluster , and various other spacecraft, mainly near 1 AU, but with also some observations from 0.3 to 4 AU up to now. The observed particle distributions are not Maxwellian, but show distinguishable structures. The physical processes that regulate the shape of particle distribution functions in the super‐Alfvénic solar wind include plasma heating/instabilities, particle collisions and adiabatic particle motion. The main constituents of the solar wind, protons, electrons and alpha particles, can develop highly anisotropic velocity distribution functions. In this chapter, we illustrate these effects by considering electrons only and refer the reader to other reviews of the field of ‘ion kinetics’ that is not discussed here (e.g. Matteini et al. 2012). Electron distributions usually consist of a thermal core, an extended suprathermal halo, and an anti‐sunward beam or “strahl” (Lin, 1974; Pilipp et al., 1987). Core and halo distributions often show temperature anisotropies, that is, different temperatures T ∥parallel to the background magnetic field, and T ⊥perpendicular to it. The temperatures of electron distributions can be determined by fits with bi‐Maxwellian or bi‐kappa distributions to core and halo components, the latter after subtraction of the asymmetric strahl component (Ogilvie et al., 2000). The different components of the electron distributions are illustrated in Figure 1.16.

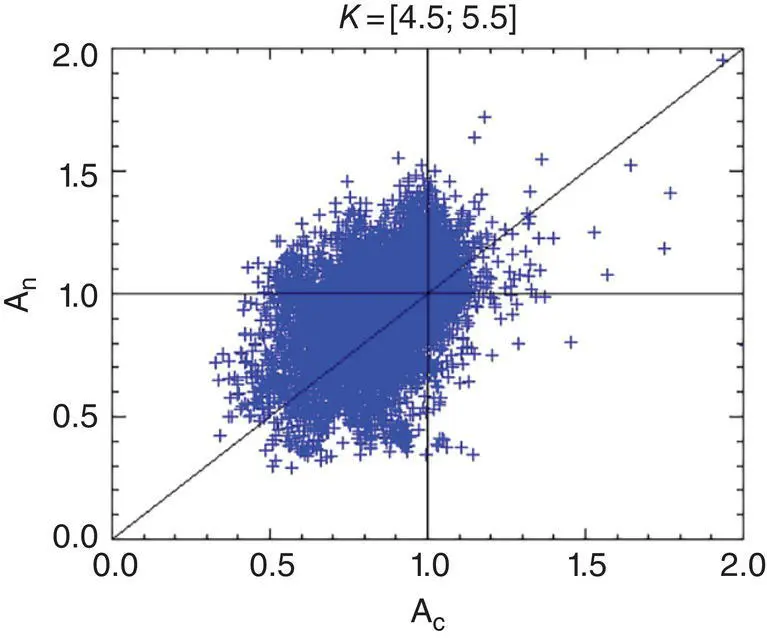
Figure 1.15 Electron temperature anisotropy of the halo ( A h= T h⊥/ T h∥) as a function of the temperature anisotropy of the electron core ( A c= T c⊥/ T c∥) observed in the solar wind with Helios , Cluster , and Ulysses from 0.7 to 1.5 AU for kappa values ranging between 4.5 and 5.5.

( Source : From Pierrard et al., 2016. © 2016, Springer Nature.)

A naive expectation for an electron distribution in the expanding solar wind would be focusing into the magnetic field direction, caused by the mirror force in the expanding magnetic field geometry of the Parker spiral. This would lead to a pronounced temperature anisotropy T ∥> T ⊥. However, this is not observed, Figure 1.15displays temperature anisotropies measured in the inner heliosphere and shows that even T ⊥ > T ∥ is frequently measured in situ in the inner heliosphere. This observation alone already indicates that processes must be active in the solar wind that are capable of increasing T ⊥relative to T ∥.

Early observations (Pilipp et al., 1990) have revealed that T ∥> T ⊥is dominant in the fast solar wind, whereas T ⊥> T ∥is more commonly found in slow solar wind streams. An extensive review of solar wind electron temperature anisotropies for solar distances between 0.3 AU and 4 AU has been provided by Pierrard et al. (2016). Core and halo electron temperature anisotropies, A cand A h, with A = T ⊥/ T ∥, are generally correlated, but their values are widely scattered between 0.5 and 2 (see Figure 1.15). Generally, A c< 1 and A h< 1, but instances with A c> 1 and A h< 1, and vice versa, are observed. The latter case, A c< 1 and A h> 1, then is much more common.

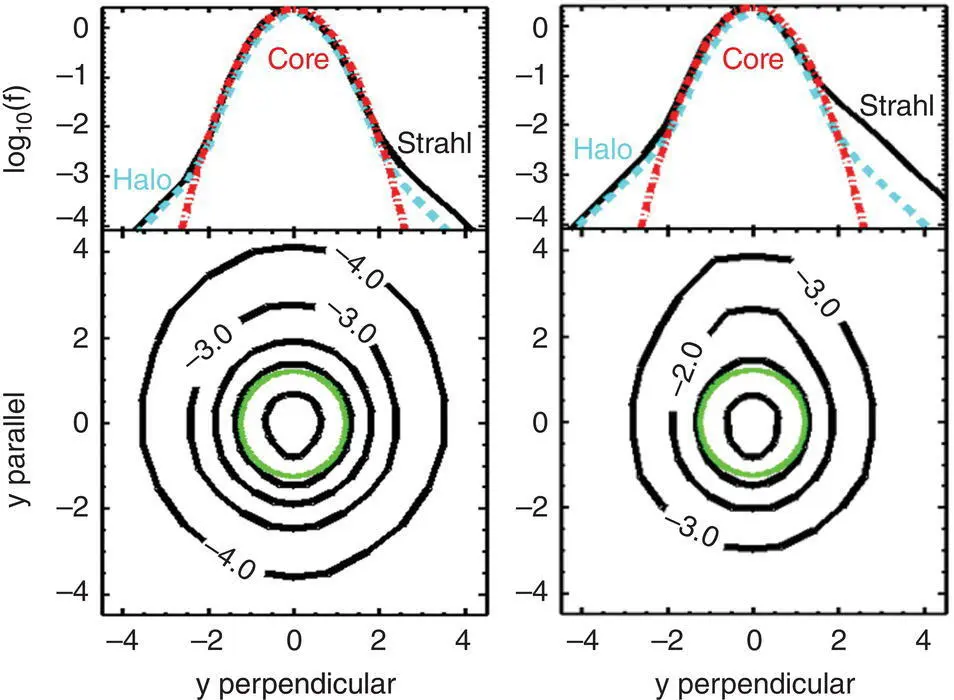
Figure 1.16 Typical electron velocity distribution function (VDF) observed by WIND at 1 AU in the low‐speed (left) and in the high‐speed (right) solar wind. Bottom panels: The plane of velocities (normalized to the thermal velocity) parallel and perpendicular to the interplanetary magnetic field. Top panels: Parallel (solid black line) and perpendicular (dashed blue line) cross section of the observed VDF. The dashed‐dotted red line represents the Maxwellian distribution that well fits the core of observed VDF.

( Source : From Pierrard, 2011. © 2011, Springer Nature.)

The maximum range of values for temperature anisotropies is constrained by the onset of plasma instabilities. A > > 1 values are unstable toward the generation of whistler waves, and A < < 1 values are subject to the firehose instability (Gary 1993). A > > 1

This picture is similar for solar wind proton distributions. They frequently show temperature anisotropies T ⊥> T ∥plus an anti‐sunward beam (see Marsch, 2012, for a review based on Helios data covering solar distances between 0.3 AU and 1 AU). The temperature anisotropy, A, shows a strong correlation with the observed ion cyclotron wave power, which indicates that the distributions are shaped by wave–particle interactions. As for electrons, the temperature anisotropies are constrained by thresholds for firehose and mirror instabilities, but are hardly observed near these limits. Observations suggest that temperature anisotropy instabilities may play a role in controlling the level of temperature anisotropy.

The low density of the solar wind plasma could lead to the expectation that it could be described as collisionless; that is, Coulomb collisions are negligible. Nevertheless, Coulomb collisions do play a role in constraining temperature anisotropies (Pierrard et al., 2016; Pierrard et al., 2011; C. Salem et al., 2003; Štverák et al., 2008)

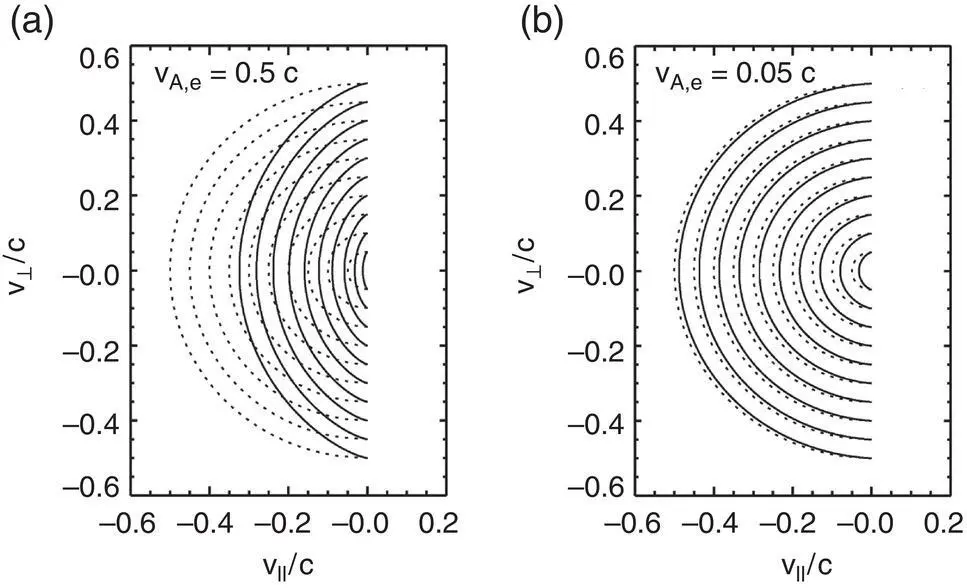
Figure 1.17 Kinetic shells formed in the electron VDF by resonant electron–whistler interaction (solid lines), and isolines of an undisturbed Maxwellian VDF (dotted lines). Shown are two plots for different values of the electron Alfvén speed, v A,e= 0.5 c (left, (a)), and v A,e= 0.05 c (right, (b)).

( Source : From Vocks & Mann, 2003. © 2003, IOP Publishing.)

Non‐Maxwellian particle distributions can become unstable toward numerous plasma instabilities (Štverák et al., 2008). Quasi‐linear theory (Kennel & Engelmann, 1966) is a useful tool to study the effect of whistler waves on the evolution of solar wind electron distributions. It considers nonlinear effects between plasma waves and the fluctuations they cause in the plasma, and therefore diffusion terms are included in the Boltzmann–Vlasov equation. Solar wind models including the effects of whistler wave turbulence are capable of reproducing the observed characteristics of solar wind electrons (Pierrard et al., 2011; Vocks, 2012).