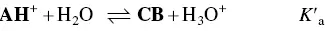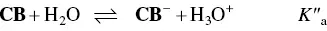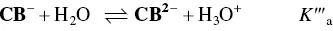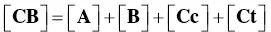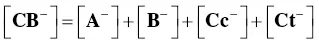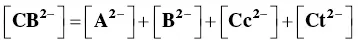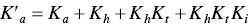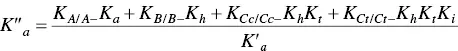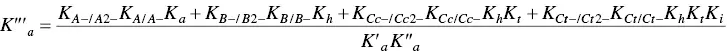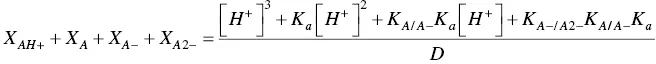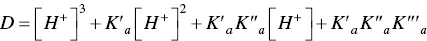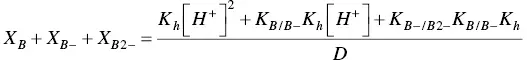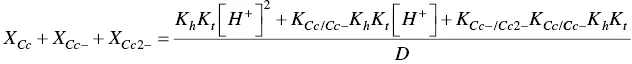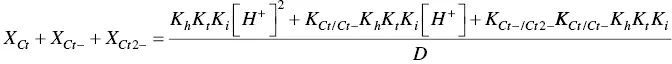Recent Advances in Polyphenol Research

In order to account for these new species, eight equilibrium equations should be added to eq. (1)through eq. (4).

For the formation of the mono‐anionic species 1

(5)

(6)

(7)

(8)

And for the formation of the di‐anionic species

(9)

(10)

(11)

(12)

The system can be generalized for higher charged anionic species.

In spite of the complexity of this system, the set of eqs. 1through 12can be simplified considering a triprotic acid, eq. (13)through eq. (15), with constants K ’ a, eq. (19) K ” a, eq. (20), and K ”’ a, eq. (21). The complete mathematical development of the system above was previously reported (supplementary information, Mendoza et al. 2019) and is straightforwardly obtained from a mass balance and representation of all species as a function of AH +.

(13)

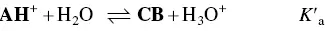
(14)

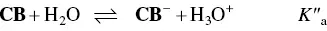
(15)

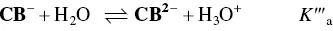
Where

(16)

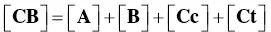
(17)

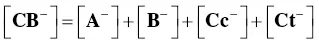
(18)

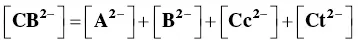
and

(19)

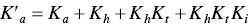
(20)

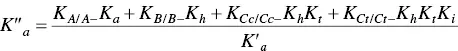
(21)

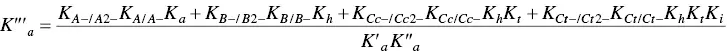
The mole fraction distribution X Rof all species can be expressed in terms of the 12 linearly independent constants reported in Scheme 1.3. Since the flavylium cation and the quinoidal bases are in very fast equilibrium (microseconds scale), it is convenient to consider them altogether. The same is valid for the other species related through the proton transfer reaction.

(22)

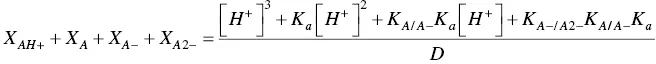
where

(23)

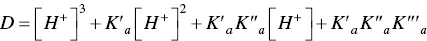
(24)

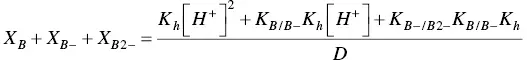
(25)

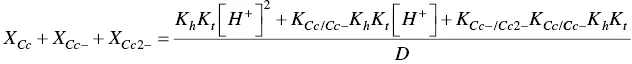
(26)

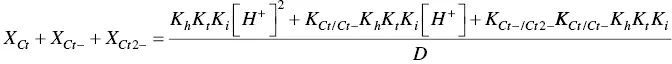
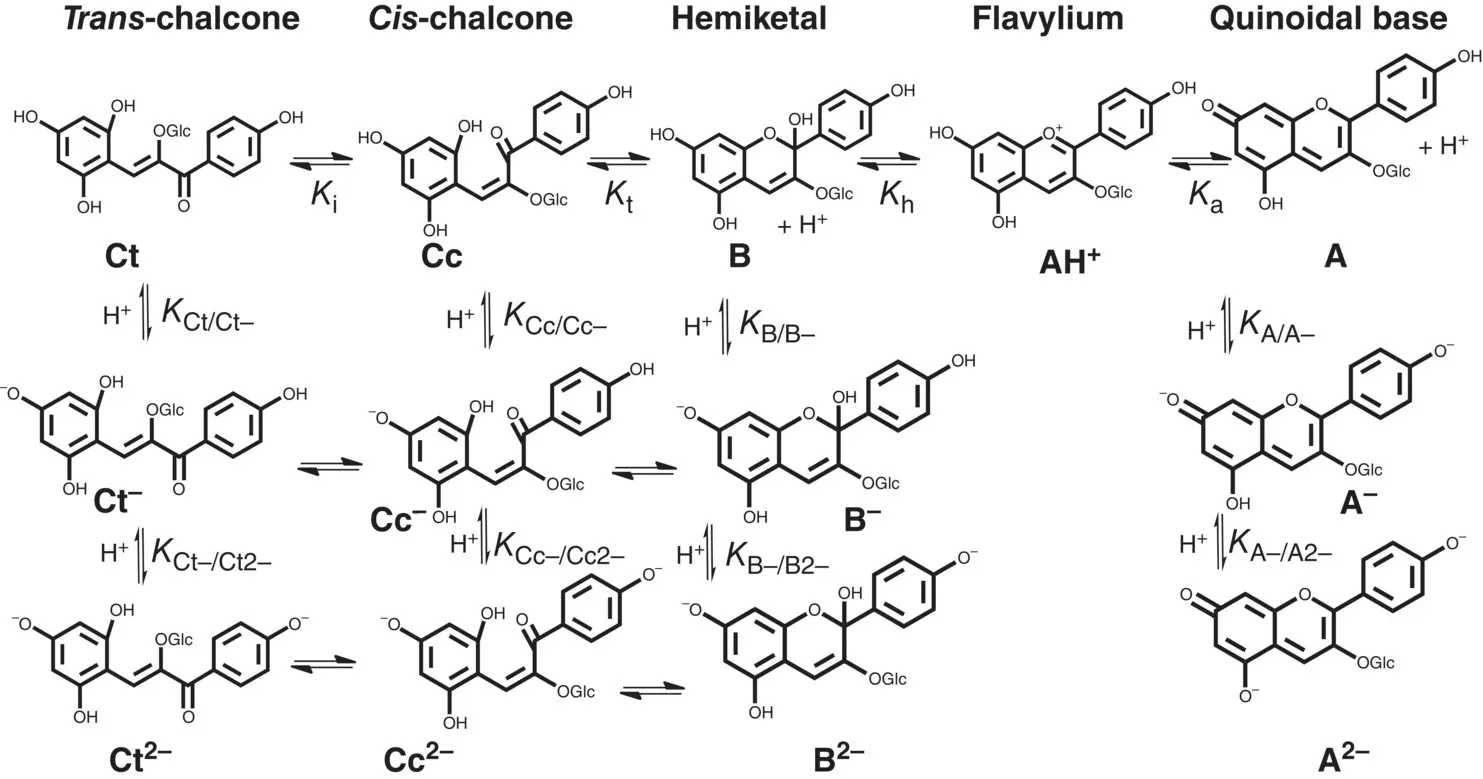
Scheme 1.3 Extension to the basic medium of Pelargonidin‐3‐glucoside.

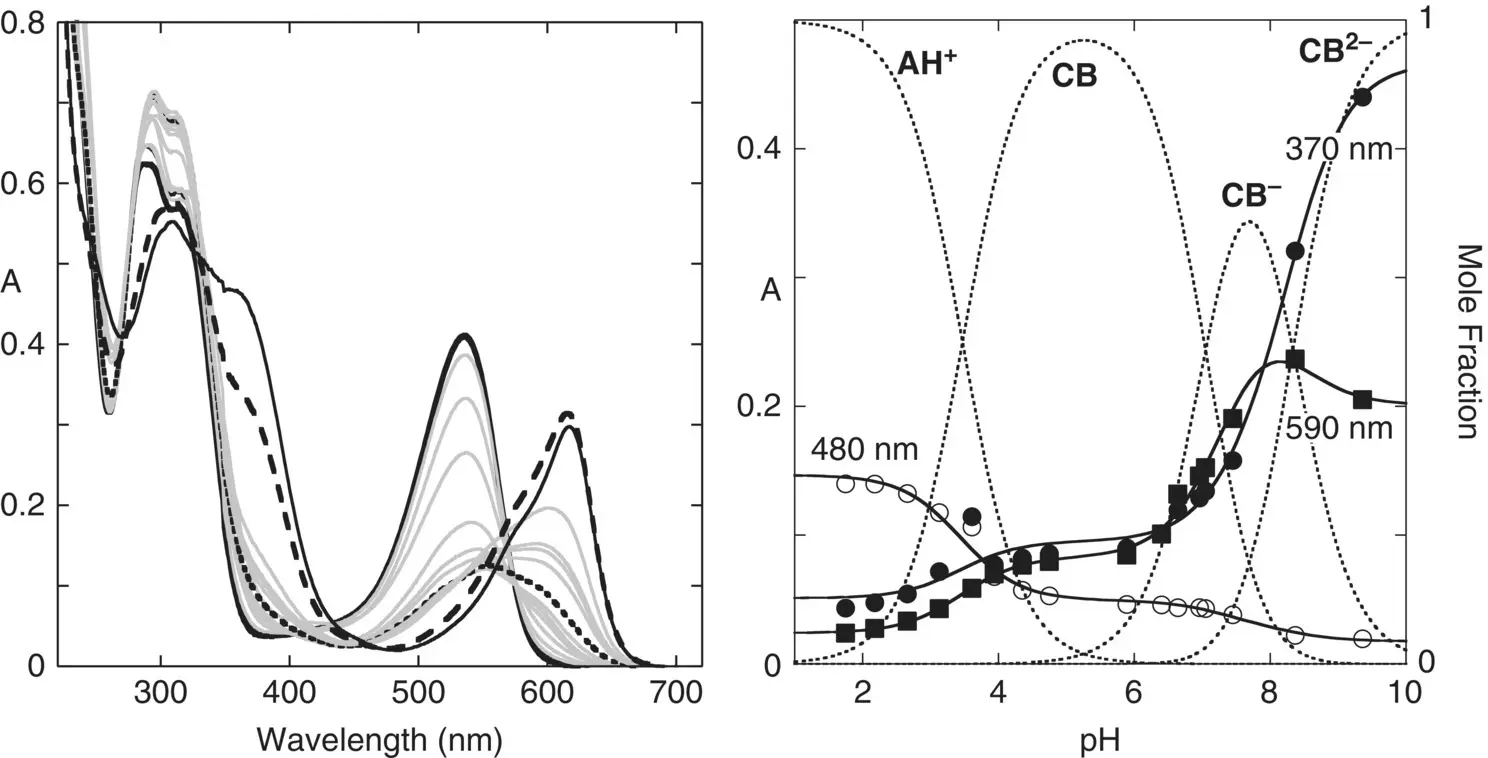
Figure 1.2 Absorption spectrum of heavenly blue anthocyanin, a peonidin derivative, black full line, flavylium cation; black pointed line, quinoidal base; black traced line, ionized quinoidal base. p K ’ a=3.47; p K ” a=7.05; p K ”’ a=8.30.

Source: Mendoza et al. 2018.

Since the complex system shown in Scheme 1.3behaves as a simple triprotic acid, the respective apparent equilibrium constants K ’ a, K ” a, and K ”’ aare experimentally obtained from the inflection points of the absorbance representation as a function of the pH. Consequently, the term Dis a parameter obtained experimentally. In Figure 1.2the example of the heavenly blue anthocyanin is shown (Mendoza et al. 2018).

The question now is to define the experimental strategy to calculate the equilibrium constants of the system.

Recently we have reported a new experimental procedure that allows the experimental determination of all equilibrium constants (as shown in Scheme 1.3) of the flavylium‐based multistates including anthocyanins (Mendoza et al. 2019; Mendoza et al. 2018; Slavcheva et al. 2018). It is based on the reverse pH jumps defined above, followed by stopped flow. In Figure 1.3the stopped flow traces of the model compound 4’‐hydroxyflavylium are shown. The initial solutions should be equilibrated or pseudo‐equilibrated. The reverse pH jumps consist of the addition of acid to make the solutions with pH=1, where flavylium cation is the sole species. In both cases of Figure 1.3the initial absorbance is due to the quinoidal bases (independently on their protonation state) that give flavylium cation (absorption at 450 nm) during the mixing time of the stopped flow together with some flavylium cation present at the initial equilibrium (at lower pH values) prior to the jump; see also Scheme 1.3. This is the reason why the mole fraction distribution of the flavylium cation and quinoidal bases are represented together in eq. (22). At the final very low pH jump (pH=1) the hydration reaction becomes faster than the tautomerization because it is directly proportional to the proton concentration (Pina 2014b). Therefore, the faster trace is due to the conversion of Binto AH +. The slower trace is the formation of more flavylium cation from Ccvia B( Scheme 1.4) (Mendoza et al. 2019).