Modern Trends in Structural and Solid Mechanics 3

The quantities in the square brackets represent concentrations. JGlyc , JResp and Jcons are the respective fluxes of glycolysis, mitochondrial respiration and ATP consumption in other cellular processes, derived phenomenologically. q 1is the fission rate, k 1and k 2are the respective synthesis rates, and d 1and d 2are the respective degradation rates. p 1to p 12are the rate constants. Even at the micro-level of the elements shown in Figure 1.2, optimal performance requires a balance between numerous processes governed by coupled equations of the form of equation [1.1].

System biology modeling approaches address such complex interactions between components of the mitochondria, leading to the fission–fusion cycles, as well as oscillations in concentrations of ATP and Ca 2+. They also address how small perturbations in biochemical concentrations result in very different fates, implying that bistability exists. Such bistability indicates “choices” in the biological processes. Feedback and feedforward loops exist to control and optimally balance the fission–fusion cycles, as well as the ATP production machinery.

Furthermore, the key proteins involved in mitochondrial dynamics are regulated in direct response to the bioenergetic state of the mitochondria. Three members of the dynamin family, which are GTPase enzymes, critical for many cell functions, are key components of the fission and fusion machineries (van der Bliek et al . 2013). We still have only a limited knowledge of the mitochondrial proteome, its entire set of proteins, but expect it to be customized and optimized to the location in the body.

Mitochondrial health (Patel et al . 2013) has been linked to its membrane potential, making it useful as an equivalent measure of health, an indicator of the effectiveness of the electron transport chain, the number of ATPases using the membrane potential, the proton leaks across the inner mitochondrial membrane and other geometric factors. Optimal mitochondrial health is linked to autophagy and fusion, the balance between fission and fusion, and the density of mitochondria in the cell.

Existing limited models of abnormal mitochondrial dynamics are insufficient to explain phenotypic variability – the aggregate of an organism’s observable characteristics – in symptoms. The mechanisms of mitochondrial functions across multiple levels of organization – molecular and organelle levels – are needed (Eisner 2018). The current, mostly descriptive representations cannot accurately model multivariate dynamics since physiological and pathological processes result from biochemical, morphological and mechanical dynamics at more than one scale, and we do not fully understand these.

The primary sites of neuronal energy consumption are at the synapses (pre and post), where mitochondria need to congregate and adapt to local energy needs. They do this via feedforward and feedback regulatory mechanisms known as mitochondrial plasticity, where adaptations to neuronal energy states occur via changes in morphology, function and position (Rossi and Pekkurnaz 2019). Mitochondrial distribution and dynamics are regulated at the molecular level by mitochondrial and axonal cytoskeleton tracks. A motor–adaptor complex exists on the mitochondrial surface that contains the transport motor proteins kinesin and dynein. Proteins Miro and Milton mostly govern mitochondrial movement (Schwarz 2013), and multiple signaling pathways converge to tailor mitochondrial positioning (Rossi and Pekkurnaz 2019). A constrained optimization framework may be used to model mitochondrial movement via an evolutionarily refined weighting mechanism. Similarly, immediate energy needs at synapses result in mitochondrial plasticity, in a mechanism for the constrained optimization of energy availability and use, where it is most needed.

The matching of energy supply to demand is evolutionarily conserved, where the organelle and the cell must optimize energy use locally and globally to ensure that balance. Where there are shortfalls in energy, the “optimal” choice may become a dysfunctional pathway, resulting in pathologies and neurodegenerative diseases. Mathematical models that incorporate data can represent the optimal choices and be powerful tools for a systematic understanding.

The mechanical aspects of cellular, mitochondrial and organelle dynamics are coupled with numerous biochemical processes that are related to healthy cell functioning, as well as to pathological developments (Feng and Kornmann 2018). Examples include mechanosensitive ion channels, curvature sensing proteins and force sensing by the cytoskeleton and plasma membrane. Organelles exchange metabolites and information by moving around the cytoplasm and coming into physical contact with each other. This intermingling appears to be an important feature for the proper functioning of eukaryotic cells. Biological phenomena observed at organelle contact locations, for example, reticulum-induced mitochondrial fission, are at least partially attributable to mechanical stimulation (Feng and Kornmann 2018).

In addition, many chemicals can alter the mechanical properties of living cells (Lim et al . 2006), indicating that certain cellular mechanical properties can be used as indicators of health. An understanding of mechanosensitive signaling pathways is fundamental (Moeendarbary and Harris 2014; Petridou et al . 2017) for the development of clinical diagnostics, as well as therapeutically successful interventions.

The mitochondria connect physically with other organelles within the cell. These interactions occur randomly in part, but are also driven by the microenvironment. The endoplasmic reticulum (ER) (also a tubular organelle) and the mitochondria tether to each other via interacting proteins situated on opposing membrane faces. Reciprocal communications transmit danger signals that can trigger multiple, synergistic responses. If needed, the number of ER–mitochondrial contact sites can be increased to allow for enhanced molecular transfers. This interface provides a platform for the regulation of different processes, such as the coordination of calcium transfers, the regulation of mitochondrial dynamics, the regulation of inflammasome formation, morphological changes and the provision of membranes for autophagy (Giorgi et al . 2009; Marchi et al . 2014).

One example of such critical coupling is the oscillations between Ca 2+concentrations in the mitochondria and the ER (Figure 1.3). These concentrations are a ubiquitous intracellular signaling mechanism for numerous cell functions. As examples, we cite neurotransmitter release from neurons and astrocytes, and metabolic processes. Interestingly, signaling information is stored in the oscillation characteristics, in particular, frequency, amplitude and duration. The aforementioned coupling, i.e. the crosstalk of Ca 2+ions, occurs within an optimal microdomain, with approximately 50 nm of spacing between a receptor and a uniporter – a membrane protein that is specialized to transport a particular substrate species across a cell membrane. At a critical distance, an optimal amount of Ca 2+released by the ER is taken up by the mitochondria, resulting in the successful generation of Ca 2+signals in healthy cells (Qi et al . 2015, see Figures 1.4 and 1.5).

In this study, optimal microdomain distances were found by varying parameter values in first-order Ca 2+flux differential equations (represented in the concentration flows in Figure 1.3(c)). The dynamic behavior is a result of a constrained optimization.

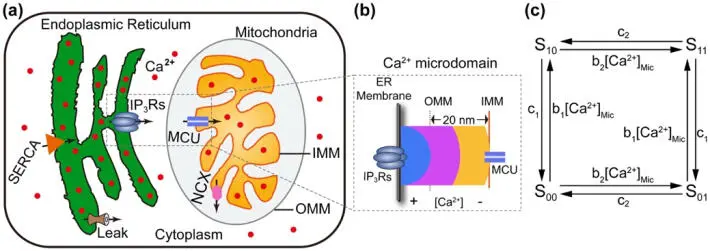
Figure 1.3. The schematic diagram of the components and fluxes included in the crosstalk model between endoplasmic reticulum and mitochondria for Ca 2+ oscillations: (a) endoplasmic reticulum (ER) and mitochondria in the cytoplasm, (b) microdomain showing activity between the ER and mitochondria, (c) four-state model with binding and unbinding rates (Qi et al. (2015), with permission). For a color version of this figure, see www.iste.co.uk/challamel/mechanics3.zip