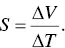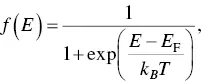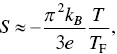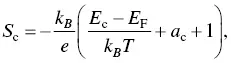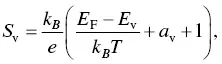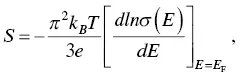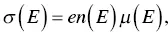To develop materials with high thermoelectric properties, good understanding in the Seebeck coefficient, electrical conductivity, and thermal conductivity is needed. Although the knowledge acquired from the study of inorganic thermoelectric materials is often used, it is not always true for organic thermoelectric materials.
1.1.1 Thermoelectric Effect
There are three thermoelectric effects, that is, Seebeck effect, Peltier effect, and Thomson effect. Correspondingly, there are Seebeck coefficient, Peltier coefficient, and Thomson coefficient. The Seebeck and Peltier coefficients are usually used for the thermoelectric generation and cooling, respectively. The Thomson coefficient is used because of the temperature dependence of the Seebeck coefficient. The three coefficients are related, and the Seebeck coefficient is the most popular term used in literature.
Thermoelectric materials are usually referred to electronic materials with high Seebeck coefficient. When there is a temperature gradient between the two ends of a thermoelectric material, a voltage will be generated between the two ends. This effect was first discovered by Alessandro Volta in 1794 and independently rediscovered by Thomas J. Seebeck in 1821. The Seebeck coefficient ( S ) is determined by the voltage (Δ V ) and the temperature gradient (Δ T ),
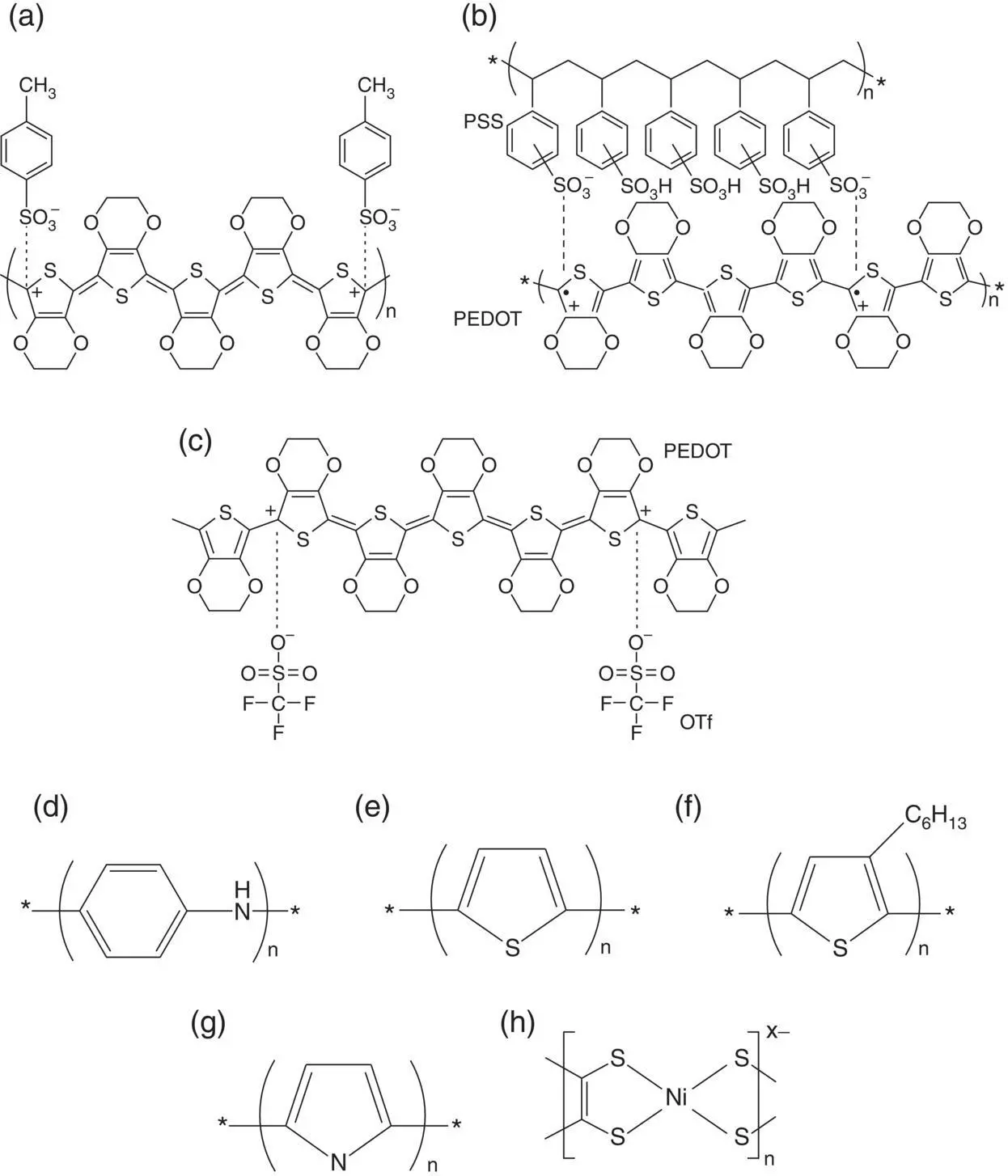
Figure 1.2 Chemical structures of some representative conducting polymers: (a) poly(3,4‐ethylenedioxythiophene):tosylate (PEDOT:Tos), (b) poly(3,4‐ethylenedioxythiophene): polystyrene sulfonate (PEDOT:PSS), (c) poly(3,4‐ethylenedioxythiophene): trifluoromethanesulfonate (PEDOT:OTf), (d) polyaniline (PANI), (e) polythiophene (PTh), (f) poly(3‐hexylthipohene) (P3HT), (g) polypyrrole (PPy), and (h) poly(nickel‐ethylenetetrathiolate) [poly(Ni‐ett)].
(1.1) 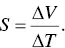
The Seebeck effect can be understood in terms of the temperature effect on the charge carrier distribution. For example, the electrons of a metal follow the Fermi–Dirac distribution,
(1.2) 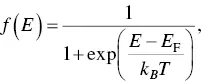
where E is the electron energy and k Bthe Boltzmann constant. The electron distribution near the Fermi level is affected by temperature. The f ( E ) value at E Fis 1 at 0 K and less than one at a temperature above 0 K. Consider two different temperatures, T Hand T C, at the two ends of a metal, the Fermi–Dirac distributions at the two temperatures are shown in Figure 1.3. When the temperature ( T C) at the cold side is 0 K, the states above the Fermi level is completely empty, while all the states below the Fermi level is fully occupied. At the hot side, the temperature ( T H) is greater than 0 K. Thus, in terms of the Fermi–Dirac distribution, some states at the energy above E Fis occupied, while some states below the Fermi level are vacant. As a result, electrons with the energy higher than E Fwill diffuse from the hot side to the cold side, while the electrons with the energy lower than E Fwill migrate in the opposite direction. But the electron diffusions along the two directions are not equivalent. At equilibrium, some electrons accumulate at the hot or cold side, this leads to an internal electric field and a voltage between the two sides. If the electrons accumulate at the cold side, the potential of the cold side will be lower than the hot side. This will lead to a negative Seebeck coefficient, and the material is an n ‐type thermoelectric material. Instead, if the electrons accumulate at the hot side, the cold side has a potential higher than the hot side. The Seebeck coefficient is positive, and it is a p ‐type material.
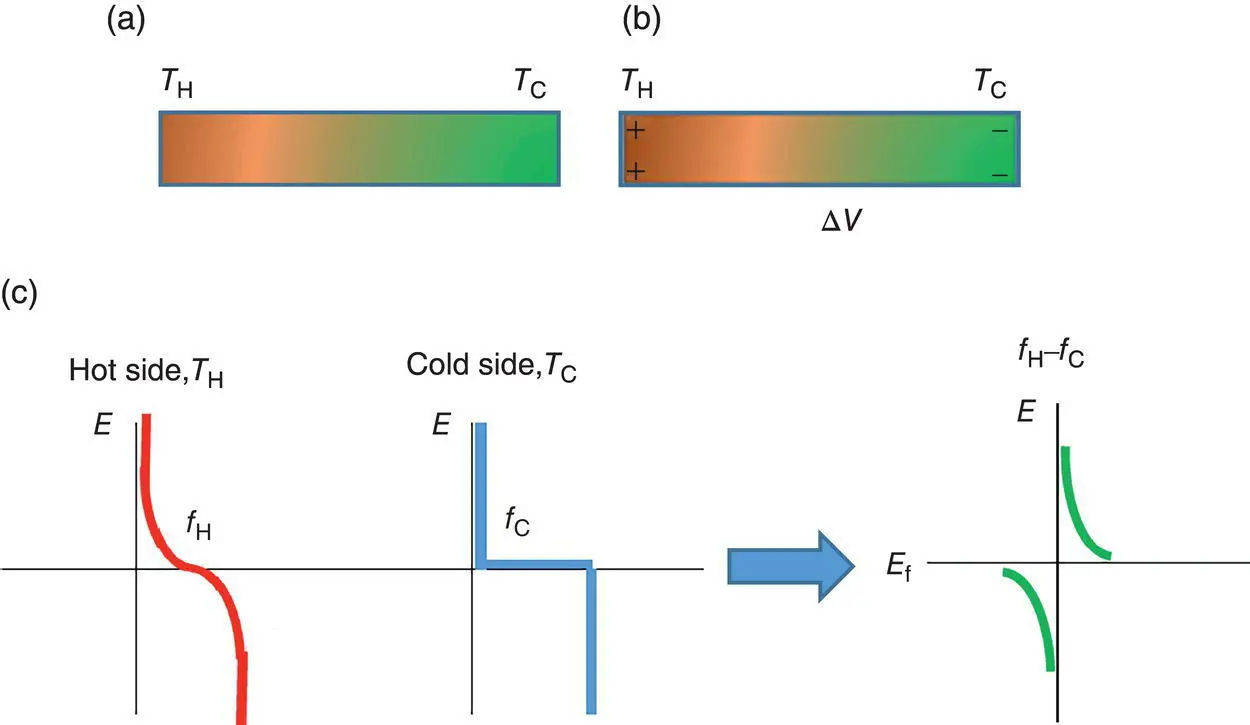
Figure 1.3 (a) A metal with different temperatures at the two sides. (b) Voltage between the two sides induced by temperature gradient. (c) Fermi–Dirac distributions at two different temperatures of T Hand T Cand their difference.
By using the Fermi gas model, the Seebeck coefficient of metals is
(1.3) 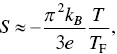
where T Fis the Fermi temperature. This is the Mott formula in metals. In terms of this formula, metals usually have small Seebeck coefficient because of their large T Fvalue of 10 4−10 5K. The absolute Seebeck coefficient values of metals are usually less than 10 μV K −1( Table 1.1).
The Seebeck coefficient of semiconductors depends on the doping level. For nondegenerated semiconductors, Eqs. (1.4)and (1.5)are the Mott formulae for the Seebeck coefficients in the conduction band and valence band, respectively,
(1.4) 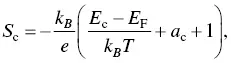
(1.5) 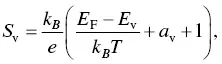
where E cis the minimum energy of the conduction band, E vis the maximum energy of the valence band, and a cand a vare constants and they depend on materials. In terms of the Mott formulae in semiconductors, the Seebeck coefficient has the maximum value when a semiconductor is lightly doped.
Table 1.1 Seebeck coefficient of some metals, semiconductors, flexible materials at room temperature.
| Metal |
S (μV K −1) |
Semiconductor |
S (μV K −1) |
Flexible materials |
S (μV K −1) |
| Sb |
+47 |
Se |
+900 |
PEDOT:PSS |
+14–20 |
| Mo |
+10 |
Te |
+500 |
PEDOT:Tso |
+30 |
| Ag |
+6.5 |
Si |
+440 |
PA |
+10 |
| Cu |
+6.5 |
Ge |
+300 |
PPy |
+10 |
| Hg |
+0.6 |
Sb 2Te 3 |
+185 |
PANi |
+10–20 |
| Pt |
+0.0 |
Pb 3Ge 39Se 58 |
+1670 |
Poly(Ni‐ett) |
−125 |
| Ni |
−15 |
Pb 15Ge 37Se 58 |
−1990 |
graphene |
−10 |
| Bi |
−72 |
Bi 2Te 3 |
−230 |
Carbon nanotube |
+20 |
For degenerated semiconductors, the Seebeck coefficient is given by
(1.6) 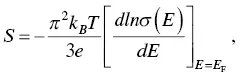
(1.7) 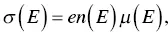
Читать дальше