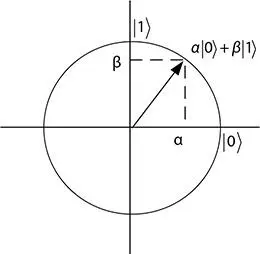
Figure 4.6 Visualization of a qubit state.
A classical machine device for quantum computing has a two-state system: 0 ↔ 1. The state of a quantum bit known as qubit is generally represented by the expression: α|0〉 + β|1〉, in which α and β are complex numbers which agree with |α| 2+ |β| 2= 1. Thus, a qubit state is represented as a unit vector in a set of complex numbers which is known as the two-dimensional complex vector space shown in Figure 4.6. The vector  may be expressed as α|0〉 + β|1〉 in quantum computing where
may be expressed as α|0〉 + β|1〉 in quantum computing where 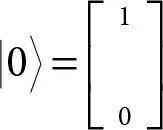 and
and 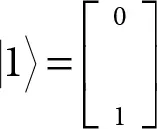 .
.
Quantum computing is totally different from most different branches of science therein it uses complex numbers in an elementary way. Quantum computing is driven through the language of complex vector space which is the set of vectors of a fixed length with complex entries. These vectors describe the states of quantum systems and quantum computers. The important role of complex vector spaces in quantum computing is described in the references [14–16].
This chapter discussed modular arithmetic, complex number arithmetic, matrix algebra, and elliptic curve arithmetic to create non-linear cryptographic transformations by using the integration of their mathematical properties. The intelligent computing on the complex plane based on the integration of complex number arithmetic with modular arithmetic is beneficial to the cryptographic applications. The proposed techniques need double the memory areas to store the keys however their security levels are generally squared. The complex plane supports the non-linear cryptographic transformations not only for traditional ciphers and elliptic curve cryptography but also for quantum cryptography in order to get more secure for sustainable development. This chapter points to the importance of complex plane in the modern cryptography.
1. Aung, T.M. and Hla, N.N., Implementation of Elliptic Curve Arithmetic Operations for Prime Field and Binary Field using java BigInteger class. Int. J. Eng. Res. Technol. (IJERT) , 6, 08, 454–459, India, 2017.
2. Aung, T.M. and Hla, N.N., A New Technique to Improve the Security of Elliptic Curve Encryption and Signature Schemes. LNCS (FDSE-2019) , vol. 11814, Springer, Cham, pp. 371–382, 2019.
3. Aung, T.M. and Hla, N.N., A Complex number Approach to Elliptic Curve Cryptosystems over Finite Fields: Implementations and Experiments. Int. Conf. Comp. Comm. Inform. (ICCCI) , IEEE, Coimbatore, Tamil Nadu, India, pp. 221–228, 2019.
4. Forouzan, B.A., Elliptic Curve Cryptosystems, in: Cryptography and Network Security , International Edition, pp. 321–330, McGraw-Hill press, Singapore, 2008.
5. Forouzan, B.A., Mathematics of Cryptography, in: Cryptography and Network Security , International Edition, pp. 98–117, McGraw-Hill press, Singapore, 2008.
6. Hankerson, D., Menezes, A., Vanstone, S., Elliptic Curve Arithmetic, in: Guide to Elliptic Curve Cryptography , pp. 75–152, Springer Verlag, New York, USA, 2004.
7. Hla, N.N. and Aung, T.M., Implementation of Finite Field Arithmetic Operations for Large Prime and Binary Fields using java BigInteger class. Int. J. Eng. Res. Technol. (IJERT) , 6, 08, 450–453, India, 2017.
8. Hla, N.N. and Aung, T.M., Attack Experiments on Elliptic Curves of Prime and Binary Fields, in: AISC (IEMIS-2018 , vol. 755, pp. 667–683, Springer, Singapore, 2019.
9. Hla, N.N. and Aung, T.M., Computing and Analysis of Residue Matrices over Complex Plane for Cryptographic Applications. Int. Conf. Comp. Info. Tech. (ICCIT-1441) , IEEE, Saudi Arabia, 2020.
10. Kreyszig, E., Complex Numbers and Their Geometric Representation, in: Advanced Engineering Mathemtics , 10th edition, pp. 608–612, John Wiley & Son Inc, USA, 2011.
11. Mohamed, E. and Elkamchouchi, H., Elliptic Curve Cryptography over Gaussian Integers. Int. J. Comput. Sci. Netw. Secur. (IJCSNS) , 4, 1, 413–416, Korea, 2009.
12. Rosen, K.H., Number Theory and Cryptography, in: Discrete Mathematics and its Applications , 7th ed, pp. 237–294, McGraw-Hill press, New York, USA, 2011.
13. Rabah, K., Elliptic Curve ElGamal Encryption and Signature Schemes. Inf. Technol. J. (ITJ) , 4, 3, 299–306, Pakistan, 2005.
14. Yanofsky, N.S. and Mannucci, M.A., Complex Numbers, in: Quantum Computing for Computer Scientists , pp. 7–15, Cambridge University Press, Cambridge, UK, 2008.
15. Yanofsky, N.S. and Mannucci, M.A., Complex Vector Spaces, in: Quantum Computing for Computer Scientists , pp. 29–66, Cambridge University Press, Cambridge, UK, 2008.
16. Yanofsky, N.S. and Mannucci, M.A., Basic Quantum Theory, in: Quantum Computing for Computer Scientists , pp. 103–132, Cambridge University Press, Cambridge, UK, 2008.
17. Yanofsky, N.S. and Mannucci, M.A., Cryptography, in: Quantum Computing for Computer Scientists , pp. 262–283, Cambridge University Press, Cambridge, UK, 2008.
1 *Corresponding author: ni2hla@ucsy.edu.mm
2 †Corresponding author: tma.mephi@gmail.com
5
Application of Machine Learning Framework for Next-Generation Wireless Networks: Challenges and Case Studies
Satyendra Singh Yadav1, Shrishail Hiremath2*, Pravallika Surisetti2, Vijay Kumar3 and Sarat Kumar Patra4
1Department of ECE, National Institute of Technology Meghalaya, Meghalaya, India
2Department of ECE, National Institute of Technology Rourkela, Odisha, India
3Centre for Nano Science and Engineering, Indian Institute of Science, Bangalore, India
4Indian Institute of Information Technology Vadodara, Gujarat, India
Abstract
Wireless communication has become an indispensable part of today’s life. Rapid growth in information and communication technologies (ICTs) along with advances in high-performance computing has witnessed a proliferation of efficient parallel and distributed computing algorithms. Presence of these with cloud computing platforms has provided a strong ecosystem for machine learning (ML) and deep learning (DL) techniques. These help to solve many of the problems like classification, optimization, and estimation, to name a few. This chapter highlights trends in fifth-generation (5G) wireless communication and beyond. This chapter further discusses use of ML algorithms in future wireless networks. These studies are expected to provide possible solutions to major challenges in the current and forthcoming wireless technology. 5G system is also expected to provide a foundation for intelligent wireless networks to handle converged applications. ML-based signal processing algorithms have the potential to solve network issues with 5G networks, thereby paving the way to the development of beyond 5G (B5G) intelligent wireless networks. This chapter presents a unified application of data science for wireless communication and analyzes the physical layer challenges for automatic modulation classification (AMC), resource allocation, channel estimation, and millimeter wave communication. Further case studies have been carried out on AMC and channel state information (CSI) feedback in massive multi-input and multi-output (MIMO) systems. The performance of the proposed DL methods has been presented through extensive simulation results.
Читать дальше


 may be expressed as α|0〉 + β|1〉 in quantum computing where
may be expressed as α|0〉 + β|1〉 in quantum computing where 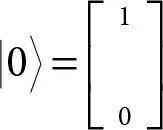 and
and 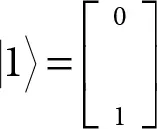 .
.










