4.6.2 Elliptic Curve Cryptography
The safety measures of “ Elliptic Curve Cryptography ” (ECC) mostly rely on the quality of solving “ Elliptic Curve Discrete Logarithm Problem ” (ECDLP). Known P and Q on the curve satisfying Q = kP , the integer k is the discrete logarithm of Q to the base P . Although P and Q are known, the group order of the curve is so huge that it is unable to compute k . It was observed in the reference [8] that elliptic curve general attacks obviously would resolve ECDLP if the group order of the curve was small enough to compute k .

Figure 4.4 Experiment on encryption.

Figure 4.5 Experiment on decryption.
The implementation and the analysis on the mathematical properties of elliptic curve arithmetic based on the integration of complex number arithmetic with modular arithmetic are described in the reference [3]. The group orders of the curves in the fields: GF ( p ), GF ( 2m), GF (2 m) Z ( GF ( p )), and Z ( GF (2 m)) were observed in the reference [2] in which the group order of the curve in Z ( GF ( p )) exposed in Appendix (C) of the reference [2] is 47 that exists between 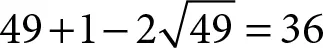 and
and 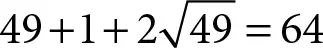 in the case of
in the case of 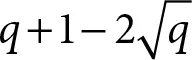 and q = p 2in accordance with Hasses’s theorem [11]. Hence, the security rank is approximately squared in terms of the group order. The attempt of resolving ECDLP on complex plane is so more computationally difficult that time duration will be long. Thus, the safety rank of ECC is significantly enhanced by using the curve of Z ( GF ( p )).
and q = p 2in accordance with Hasses’s theorem [11]. Hence, the security rank is approximately squared in terms of the group order. The attempt of resolving ECDLP on complex plane is so more computationally difficult that time duration will be long. Thus, the safety rank of ECC is significantly enhanced by using the curve of Z ( GF ( p )).
4.6.2.1 Elliptic Curve Encryption Scheme
The non-linear cryptographic transformations for encryption scheme and decryption scheme can be created by using elliptic curve arithmetic based on the integration of complex number arithmetic with modular arithmetic. The implementation is described in the reference [2].
Let us consider ElGamal encryption scheme [13] using the curve E : y 2= x 3+ x + (1 + 5 i ) over Z ( GF (7)) where a = 1 and b = 1 + 5 i . The followings are the experiments of key generation, encryption scheme, and decryption scheme executing on the given curve by using the methods implemented in the reference [2].
Key Generation . Alice and Bob are in agreement on P = (5, 3 + 2 i ) as a base point. It has prime order n = 47. Bob calculates a pair of private key and public key as followings.
• Bob defines his private key: d = 13.
• Bob calculates his public key: Q = d × P = 13 × (5, 3 + 2i) = (1 + 5i, 4 + 5i).
Encryption Scheme . Alice defines M = (2 + 5 i , 3 + 6 i ) as a message to be encrypted with Bob’s public key Q = (1 + 5 i , 4 + 5 i ). The cipher text is the result of the encryption scheme. Alice calculates the cipher text as followings.
• Alice selects a random number: r = 3.
• Alice calculates: C1 = r × P = 3 × (5, 3 + 2i) = (5 + 6i, 5).
• Alice calculates: C2 = M + (r × Q) = (2 + 5i, 3 + 6i) + 3.(1 + 5i, 4 + 5i) = (1 + 1i, 2 + 2i).
• Alice sends C1 and C2 to Bob as cipher texts.
Decryption Scheme . Bob receives C 1= (5 + 6 i , 5) and C 2= (1 + 1 i , 2 + 2 i ) as cipher texts to be decrypted with his private key d = 13. The message is the result of decryption scheme. Bob calculates the message as following.
• Bob calculates the message: M = C2 – (d × C1) = (1 + 1i, 2 + 2i) – 13.(5 + 6i, 5) = (2 + 5i, 3 + 6i).
4.6.2.2 Elliptic Curve Signature Scheme
The non-linear cryptographic transformations for signature signing scheme and signature verifying scheme can also be created by using elliptic curve arithmetic based on the integration of complex number arithmetic with modular arithmetic. The implementation is described in the reference [2].
Let us consider ElGamal signature scheme [13] using the curve E : y 2= x 3+ x + (1 + 5 i ) over Z ( GF (7)) where a = 1 and b = 1 + 5 i . The followings are the experiments of key generation, signing scheme and verifying scheme executing on the given curve by using the methods implemented in the reference [2].
Key Generation . Alice and Bob are in agreement on P = (5, 3 + 2 i ) as a base point. It has prime order n = 47. Alice calculates a pair of private key and public key as followings.
• Alice defines her private key: d = 13.
• Alice calculates her public key: Q = d × P = 13 × (5, 3 + 2i) = (1 + 5i, 4 + 5i).
Signing Scheme . Alice signs the message with her private key d = 13. The signature is the result of signing scheme. Alice calculates the signature as the followings.
• Alice selects a random number: k = 3.
• Alice calculates: R = k × P = 3 × (5,3 + 2i) = (5 + 6i,5.
• Alice calculates: r = R.x.real mod n = 5 mod 47 = 5.
• Alice calculates: h = h(m) = 4 (Hash value).
• Alice calculates: s = k−1(h + rd) mod n = 16 × (4 + 5 × 13) mod 47 = 42.
• Alice sends (R, s) to Bob as the signature of the message.
Verifying Scheme . Bob verifies the signature ( R , s ) with Alice’s public key Q = (1 + 5 i , 4 + 5 i ). The verification codes are the result of verifying scheme. Bob calculates verification codes V 1and V 2as the followings and makes a comparison of them.
• Bob calculates: V1 = s × R = 42 × (5 + 6i, 5) = (6 + 6i, 5 + 3i).
• Bob calculates: r = R.x.real mod n = 5 mod 47 = 5.
• Bob calculates: h = h(m) = 4 (Hash value).
• Bob calculates: U1 = h × P = 4 × (5, 3 + 2i) = (4 + 2i, 3 + 3i).
• Bob calculates: U2 = r × Q = 5 × (1 + 5i, 4 + 5i) = (2i, 4 + 6i).
• Bob calculates: V2 = U1 + U2 = (6 + 6i, 5 + 3i).
• Bob accepts the signature, since V1 = V2.
4.6.3 Quantum Cryptography
Modern cryptography algorithms are based on the most important method of factorization against giant integers into their primes, which is tough to be solved. But modern cryptography is at risk of each technical growth of computing power in arithmetic to quickly reverse one-way functions like that of factorization massive numbers. So, quantum computing is introduced into cryptography, which ends up in the analysis of quantum cryptography. Quantum cryptography is the science that applies quantum mechanics to carry out cryptographic tasks. Quantum cryptography is one among the emerging topics within the sector of computer industry. Quantum cryptography brings quantum key generation, quantum key distribution, quantum public key encryption, and quantum random number generation. Quantum cryptography covers the weaknesses of recent digital cryptosystems, and eventually toward the longer term direction.
Читать дальше



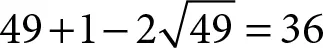 and
and 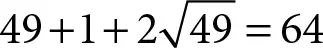 in the case of
in the case of 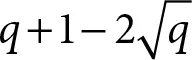 and q = p 2in accordance with Hasses’s theorem [11]. Hence, the security rank is approximately squared in terms of the group order. The attempt of resolving ECDLP on complex plane is so more computationally difficult that time duration will be long. Thus, the safety rank of ECC is significantly enhanced by using the curve of Z ( GF ( p )).
and q = p 2in accordance with Hasses’s theorem [11]. Hence, the security rank is approximately squared in terms of the group order. The attempt of resolving ECDLP on complex plane is so more computationally difficult that time duration will be long. Thus, the safety rank of ECC is significantly enhanced by using the curve of Z ( GF ( p )).










