Following intense research carried out after the Second World War, new piezoelectric materials were developed. These included notably lead zirconate titanate (PZT) ceramics, which could be made piezoelectric by applying an electric field. These materials, whose electromechanical coupling coefficient is much higher than that of quartz, greatly facilitated the generation and detection of elastic waves of frequency lower than 10 MHz. As they could be used to create sensitive transducers of large dimensions and of varied shapes, these ceramics constitute the active elements of transmitters and receivers in sonars and of medical and metallurgical ultrasonic equipment.
In 1965, R.M. White and F.W. Voltmer implemented the idea of generating and detecting surface acoustic waves using two comb-shaped electrodes deposited on a piezoelectric material. The exploitation of this technique led to a series of spectacular applications of Rayleigh waves. These surface acoustic wave filters, which are very compact, can be mass-produced owing to microelectronic technologies and operate in a wide range of frequencies (50 MHz–5 GHz). They have invaded the consumer electronics market, in products such as televisions and mobile phones. The continuous improvement in their performances required the elaboration of new piezoelectric crystals of large dimensions, as well as a finer and finer analysis of the propagation, interaction and generation of surface waves.
From the 1990s onward, we have witnessed a large-scale development of elastic waves in varied domains, such as medical imaging and therapy, non-destructive evaluation of materials, sensors of physical or biological quantities, acoustic detection and localization systems for submarines applications, and for locating and exploring oil fields. These advances have different origins, sometimes involving a combination of factors: the elaboration of composite materials and thin piezoelectric layers, the refinement of high-performance instruments (acoustic microscopes, multi-element transducers), innovative methods (time-reversal acoustics), as well as progress in computer sciences, whether for simulations or running processes. Given the scope of our current text, it is not possible to fully describe these applications, which evolve so fast.
Our objective is to provide the reader with the theoretical bases required to understand these developments, to explore them in detail and to elaborate on other advances. In order to move away from abstraction, the phenomena are illustrated by many figures corresponding to commonly used structures and materials. Furthermore, the text regularly specifies the order of magnitude of physical parameters.
The first volume is divided into four chapters and three appendices. Chapter 1deals with the propagation of elastic waves in an unbounded solid. In the absence of any boundary, the only problem is to establish the equations for the propagation of a mechanical disturbance and to solve them. However, in order to do this, the constitutive laws for the solid must be known. This solid may be isotropic, anisotropic, piezoelectric, purely elastic or viscoelastic. Chapter 2focuses on the phenomena of reflection and transmission between two semi-infinite media separated by a planar interface. The propagation equations in each medium must be supplemented by limiting conditions that ensure the connection of the physical quantities on the boundary. Several examples are treated: solid–vacuum interfaces, solid-perfect fluid and isotropic solid-anisotropic crystal. For each configuration, the analysis shows modes that exist in the absence of any incident waves; these surface and interface waves are studied in Chapter 3. A very important example is that of the semi-infinite solid, along whose surface a pure or generalized Rayleigh wave is always propagated, regardless of the material. Other waves appear at the interface between a solid and a fluid (Scholte waves), while the conditions for existence are very restrictive at the interface between two solids (Stoneley waves). When the solid is limited by several parallel planes, the successive reflections of the bulk elastic waves give rise to guided waves. The properties of these guided waves are analyzed in Chapter 4. The simplest are transverse horizontal waves, discovered by Love, which are partly propagated in a layer and partly in its substrate. Given their practical importance, the Lamb waves, with two components, progressing in a plate are treated in detail both in the case of isotropic and anisotropic solids. The propagation of these plate modes is dispersive, like that of guided waves in cylinders, studied at the end of this chapter.
The second volume investigates the properties of acoustic fields emitted by various sources of finite dimensions, the interaction of elastic waves with cylindrical and spherical targets immersed in a fluid or buried in a solid, the means of generating and detecting the waves studied in the first volume.
The authors wish to extend their gratitude to Claire Prada, Director of Research at CNRS, institut Langevin Ondes et Images, for her help during the writing of this first volume.
October 2021
a, b : amplitude of the waves.
cijkl ( CIJ ) : stiffnesses (Voigt notation).
D : directivity factor.
D : electric induction (displacement) vector.
E : Young modulus.
E : electric field vector.
ec ( ep ) : kinetic (potential) energy per unit volume.
eijk ( εij ) : piezoelectric (dielectric) constants.
F : force density per unit mass.
H ( t ) : Heaviside step function.
I : acoustic intensity.
J : Poynting vector.
K : bulk modulus.
k ( k ) : wave vector (number).
KM : electromechanical coupling coefficient (mode M).
l : unit vector normal to a surface.
n : unit vector of the propagation direction.
P : transported power.
pa : acoustic pressure.
p ( p 0) : thermodynamic pressure (at rest).
p , q : polarization vectors.
Ps ( ps ) : power supplied by the source (per unit volume).
r ( t ) : amplitude reflection (transmission) coefficients.
R ( T ) : intensity reflection (transmission) coefficients.
s : entropy per unit volume.
s : phase slowness vector.
T : absolute temperature.
T : mechanical traction, stress vector.
u : mechanical displacement vector.
U : internal energy per unit volume.
v : particle velocity vector.
V e: energy velocity vector.
V ( Vg ) : phase (group) velocity.
VL ( VT ) : velocity of longitudinal (transverse) bulk waves.
W ( w ) : work (per unit volume).
x : position vector.
X, Y, Z : crystallographic axes.
Ze ( Y ) : electrical impedance (admittance).
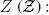 acoustic (mechanical) impedance.
acoustic (mechanical) impedance.
α : attenuation coefficient.
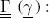 : elastic (piezoelectric) Christoffel tensor.
: elastic (piezoelectric) Christoffel tensor.
δij : Kronecker’s symbol.
δ ( t ) : Dirac function.
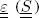 : linearized strain tensor (piezoelectric solid).
: linearized strain tensor (piezoelectric solid).
η : viscosity coefficient.
θi,r,t : angle of incidence, reflection, transmission.
Читать дальше

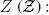 acoustic (mechanical) impedance.
acoustic (mechanical) impedance.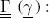 : elastic (piezoelectric) Christoffel tensor.
: elastic (piezoelectric) Christoffel tensor.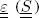 : linearized strain tensor (piezoelectric solid).
: linearized strain tensor (piezoelectric solid).










