504. Find the point(s) on the ellipse  farthest from
farthest from 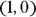 .
.
505. Find the point on the line 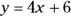 that is closest to the origin.
that is closest to the origin.
506. A rectangular poster is to have an area of 90 square inches with 1-inch margins at the bottom and sides and a 3-inch margin at the top. What dimensions give you the largest printed area?
507. At which x values on the curve 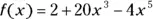 does the tangent line have the largest slope?
does the tangent line have the largest slope?
508. A rectangular storage container with an open top is to have a volume of 20 cubic meters. The length of the base is twice the width. The material for the base costs $20 per square meter. The material for the sides costs $12 per square meter. Find the cost of the materials for the cheapest such container. Round your answer to the nearest cent.
509. A piece of wire that is 20 meters long is cut into two pieces. One is shaped into a square, and the other is shaped into an equilateral triangle. How much wire should you use for the square so that the total area is at a maximum?
510. A piece of wire that is 20 meters long is cut into two pieces. One is bent into a square, and the other is bent into an equilateral triangle. How much wire should you use for the square so that the total area is at a minimum?
511. The illumination of a light source is directly proportional to the strength of the light source and inversely proportional to the square of the distance from the source. Two light sources, one five times as strong as the other, are placed 20 feet apart, and an object is placed on the line between them. How far from the bright light source should the object be placed so that the object receives the least illumination?
512. Find the area of the largest rectangle that can be inscribed in the ellipse 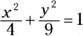 .
.
Doing Approximations Using Newton’s Method
513–515Find the fifth approximation of the root of the equation using the given first approximation.
513. 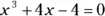 using
using 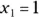 . Round the solution to the fifth decimal place.
. Round the solution to the fifth decimal place.
514. 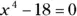 using
using 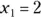 . Round the solution to the seventh decimal place.
. Round the solution to the seventh decimal place.
515. 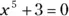 using
using 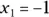 . Round the answer to the seventh decimal place.
. Round the answer to the seventh decimal place.
Approximating Roots Using Newton’s Method
516–518Find the root using Newton’s method.
516. Use Newton’s method to find the root of cos 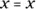 correct to five decimal places.
correct to five decimal places.
517. Use Newton’s method to find the root of 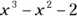 in the interval
in the interval 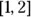 correct to five decimal places.
correct to five decimal places.
518. Use Newton’s method to find the positive root of 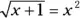 correct to five decimal places.
correct to five decimal places.
Chapter 9
This chapter provides some of the groundwork and motivation for antiderivatives. Finding the area underneath a curve has real-world applications; however, for many curves, finding the area is difficult if not impossible to do using simple geometry. Here, you approximate the area under a curve by using rectangles and then turn to Riemann sums. The problems involving Riemann sums can be quite long and involved, especially because shortcuts to finding the solution do exist; however, the approach used in Riemann sums is the same approach you use when tackling definite integrals. It’s worth understanding the idea behind Riemann sums so you can apply that approach to other problems!
The Problems You’ll Work On
This chapter presents the following types of problems:
Using left endpoints, right endpoints, and midpoints to estimate the area underneath a curve
Finding an expression for the definite integral using Riemann sums
Expressing a given Riemann sum as a definite integral
Evaluating definite integrals using Riemann sums
Here are some things to keep in mind as you do the problems in this chapter:
Estimating the area under a curve typically involves quite a bit of arithmetic but shouldn’t be too difficult conceptually. The process should be straightforward after you do a few problems.
The problems on expressing a given Riemann sum as a definite integral don’t always have unique solutions.
To evaluate the problems involving Riemann sums, you need to know a few summation formulas. You can find them in any standard calculus text if you don’t remember them — or you can derive them!
Calculating Riemann Sums Using Left Endpoints
519–522Find the Riemann sum for the given function with the specified number of intervals using left endpoints.
519.  ,
, 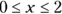 ,
, 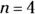
520. 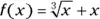 ,
, 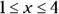 ,
, 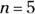 . Round your answer to two decimal places.
. Round your answer to two decimal places.
Читать дальше

 farthest from
farthest from 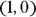 .
.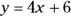 that is closest to the origin.
that is closest to the origin.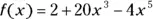 does the tangent line have the largest slope?
does the tangent line have the largest slope?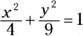 .
.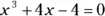 using
using 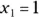 . Round the solution to the fifth decimal place.
. Round the solution to the fifth decimal place.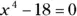 using
using 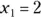 . Round the solution to the seventh decimal place.
. Round the solution to the seventh decimal place.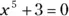 using
using 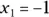 . Round the answer to the seventh decimal place.
. Round the answer to the seventh decimal place.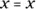 correct to five decimal places.
correct to five decimal places.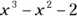 in the interval
in the interval 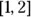 correct to five decimal places.
correct to five decimal places.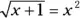 correct to five decimal places.
correct to five decimal places. ,
, 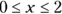 ,
, 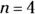
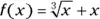 ,
, 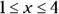 ,
, 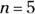 . Round your answer to two decimal places.
. Round your answer to two decimal places.










