Patrick Jones - Calculus - 1001 Practice Problems For Dummies (+ Free Online Practice)
Здесь есть возможность читать онлайн «Patrick Jones - Calculus - 1001 Practice Problems For Dummies (+ Free Online Practice)» — ознакомительный отрывок электронной книги совершенно бесплатно, а после прочтения отрывка купить полную версию. В некоторых случаях можно слушать аудио, скачать через торрент в формате fb2 и присутствует краткое содержание. Жанр: unrecognised, на английском языке. Описание произведения, (предисловие) а так же отзывы посетителей доступны на портале библиотеки ЛибКат.
- Название:Calculus: 1001 Practice Problems For Dummies (+ Free Online Practice)
- Автор:
- Жанр:
- Год:неизвестен
- ISBN:нет данных
- Рейтинг книги:3 / 5. Голосов: 1
-
Избранное:Добавить в избранное
- Отзывы:
-
Ваша оценка:
Calculus: 1001 Practice Problems For Dummies (+ Free Online Practice): краткое содержание, описание и аннотация
Предлагаем к чтению аннотацию, описание, краткое содержание или предисловие (зависит от того, что написал сам автор книги «Calculus: 1001 Practice Problems For Dummies (+ Free Online Practice)»). Если вы не нашли необходимую информацию о книге — напишите в комментариях, мы постараемся отыскать её.
.
The perfect companion to
—and your class— this book offers readers challenging practice problems with step-by-step and detailed answer explanations and narrative walkthroughs. You’ll get free access to all 1,001 practice problems online so you can create your own study sets for extra-focused learning.
Readers will also find:
A useful course supplement and resource for students in high school and college taking Calculus I Free, one-year access to all practice problems online, for on-the-go study and practice An excellent preparatory resource for faster-paced college classes
is an essential resource for high school and college students looking for more practice and extra help with this challenging math subject.
Calculus: 1001 Practice Problems For Dummies
1,001 Calculus Practice Problems For Dummies
Dummies

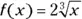 ,
, 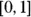
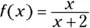 ,
, 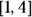
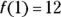 and
and 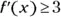 for
for  , what is the smallest possible value of
, what is the smallest possible value of 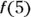 ? Assume that f satisfies the hypothesis of the mean value theorem.
? Assume that f satisfies the hypothesis of the mean value theorem.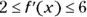 for all values of x. What are the strictest bounds you can put on the value of
for all values of x. What are the strictest bounds you can put on the value of 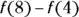 ? Assume that f is differentiable for all x.
? Assume that f is differentiable for all x.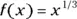 on the interval
on the interval 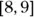 to find bounds for the value of
to find bounds for the value of 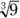 .
.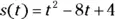 at
at 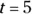
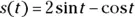 at
at 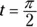
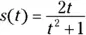 at
at 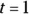
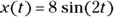 , where x is measured in feet and t is measured in seconds. Is the spring stretching or compressing at
, where x is measured in feet and t is measured in seconds. Is the spring stretching or compressing at 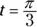 ? What is the speed of the spring at that time?
? What is the speed of the spring at that time?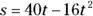 , where s is measured in feet and t is measured in seconds. What is the maximum height of the stone? What is the velocity of the stone when it’s 20 feet above the ground on its way up? And what is its velocity at that height on the way down? Give exact answers.
, where s is measured in feet and t is measured in seconds. What is the maximum height of the stone? What is the velocity of the stone when it’s 20 feet above the ground on its way up? And what is its velocity at that height on the way down? Give exact answers.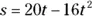 , where s is measured in feet and t is measured in seconds. What is the maximum height of the stone? What is the velocity of the stone when it hits the ground?
, where s is measured in feet and t is measured in seconds. What is the maximum height of the stone? What is the velocity of the stone when it hits the ground?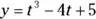 for
for 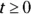 . When is the particle moving upward, and when is it moving downward? Give an exact answer in interval notation.
. When is the particle moving upward, and when is it moving downward? Give an exact answer in interval notation.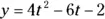 for
for 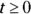 . When is the particle moving upward, and when it is it moving downward? Give your answer in interval notation.
. When is the particle moving upward, and when it is it moving downward? Give your answer in interval notation.










