George V. Chilingar - Acoustic and Vibrational Enhanced Oil Recovery

where the function fα ( ζ ) may be represented through an inverse Laplace transform:

(2.7)

Its expansion in a series is

(2.8)

where H ( ζ ) is Heaviside step function. In a special case at α = ½, the series (2.8)converges to

(2.9)

Due to nonuniform convergence of the series Equation (2.8), may also be found asymptotic formula for f α( ζ ). It is determined using the saddle point method:

(2.10)

This correlation becomes equal to the exact expression Equation (2.9)at α = 1/2.

The function f α( ζ ) defined by the equality Equation (2.7)converges to δ ( ζ ) at λ → 0. There is the equivalent representation of the last term in expression Equation (2.6)for cores of Equation (2.3)type. The packing φ α( ζ )* f α( ζ ) may be computed explicitly for this case and the left part of Equation (2.6)may then be written in a form more convenient for computation as it no longer includes the second integral. The function t = (| x | + τ | x |) is smooth and is faster tending to zero with the approach to the front corresponding to τ = 0 than nay power of τ, remaining infinitely differentiable which is obvious from (2.10).

The trivariate Green function for the medium model under review represents a solution of the spherically symmetric Cauchy problem [30]:

(2.11)

(2.12)

where

The solution of Equations (2.11)and (2.12)has the following format:

(2.13)

where it is assumed that

(2.14)

The Green’s function (2.13)behind the front ( τ ˂˂ αr ) as presented in space-time has the following format:

(2.15)

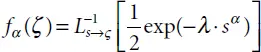
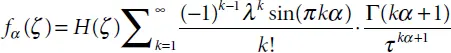
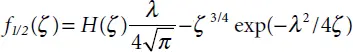
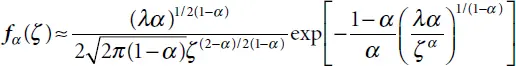
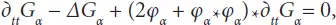
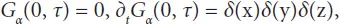
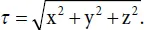
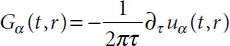
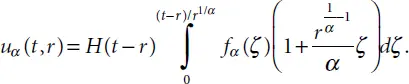
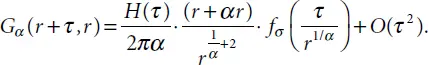
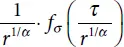According to the theory of generalized functions, tends to δ ( τ )/2 at λ → 0. The Green function G α( t,r ) shown in Equation (2.15)converges in this case to a simple Green function of the classical wave differential equation, i.e., to 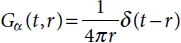. The solution at α = 1/2 may be presented in a simple explicit format: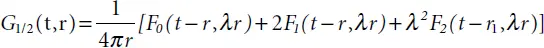

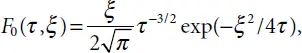
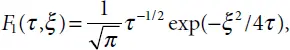
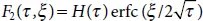
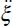(2.16)

where

(2.17)

(2.18)

(2.19)

As two independent polarization types are available in a solid isotropic medium, the total displacement vector u( r,t ) should be presented in the form of in-plane u land lateral u rdisplacements:

(2.20)

Each of these displacements may be directed by integrodifferential equation of Equation (2.11)type but with different multiplier before the terms including time derivatives due to the differences in the high frequency sound velocity limit for these two wave types. The integral terms creep cores also differ (displacement creep function and triaxial creep function). However, their time correlation is identical if identical processes lead to local relaxation. For this reason, the methods designed for scalar equations may be applied with every scalar component of every polarization displacement vector simply by scaling the derived solutions.

As an indicator of efficiency at a certain frequency may serve encompassment radius within which are maintained certain interrelations between the threshold values of vibration parameters—vibratory displacements ξ and vibratory accelerations . These parameters are determined from the density of vibratory energy flow E at a given point of the medium and through vibration frequency f as follows:

where ρC is the wave resistance or acoustic impedance of the medium.

Numerical modeling was conducted by Sherifulling et al . [26] in order to determine the vibrations’ space-energy distribution. This enabled the computation of the energy picture of the wave distribution field for the assigned vibration frequency and of the vibratory accelerations and offsets field in the reservoir accounting for petro-physical properties of the top and base of the reservoir. Modeling was conducted using a method of the wave spreading statistical testing in the plane dissecting the reservoir with the plane-parallel boundaries [20]. The source of harmonic waves was distributed along the circumference of a well with the radius R cwith the center in the origin. The top and base of a reservoir having thickness H was positioned parallel to the X axis. At calculating by the statistical testing method, the spreading of the low-frequency harmonic waves is modeled using acoustic “quanta” flying out from the source in a random direction. Acoustic energy is assigned to each “quantum”, the energy equal to surficial density of a cylindric pulsator with the pressure amplitude P 0: