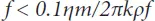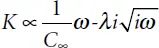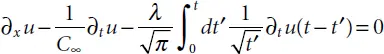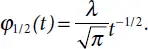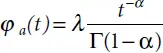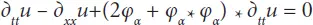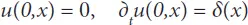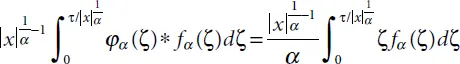1 ...7 8 9 11 12 13 ...20 Another factor affecting the wave spreading is various boundaries and rock stratification in the productive reservoirs. Experimental observations showed that in a porous medium saturated with oil, gas, or water, reflection coefficients from various fluids’ contact surfaces are comparable with reflection coefficients by geological boundaries separating different lithologies [13]. When boundaries are available with clearly expressed reflecting properties, interactions appear and energy exchange between different wave types.
At certain conditions, the medium stratification results in resonance, wave phenomena [27]. The influence of separation boundaries on wave spreading in the saturated porous media was studied by several authors. The analytical description of the reflection and refraction processes at the boundary of such media is complex. That is why only cases of flat wave normal incidence on the separation boundary of two media were studied or cases of an arbitrary incidence angle on the free surface (contact with vacuum). The problem of a flat wave at-angle incidence on the boundary corresponding with the contact of different fluids (oil, gas, and water) in a porous medium was numerically solved by Berson [1]. Insufficient knowledge of reflection and refraction processes for this case was due to a great number of parameters in the Frenkel-Bio-Nikolayevsky equations, the parameters characteristic for any specific situation. A special problem was selection of the source data for possible calculations as it was necessary, within several calculation situations, to identify specific features of wave transformation processes at the boundaries.
Within the framework of this theory, flat harmonic vertically and horizontally polarized waves within isotropic saturated layer limited by absolutely rigid semi-space were also studied [7]. Analytic formats of the fading coefficients were derived. Analytic formats for phase and group velocities of normal waves within the layer were derived. The presence of critical normal waves was established, similar to the appropriate concept of the wave theory in purely elastic wave guides near which the monotonous behavior of group velocities and fading coefficients disrupted. Thus, approximate analytical approach for the consideration of interaction between a layer (bed) with enclosing rocks and major parameters of flat monochromatic waves in the layer was used. Also, the escape of some vibration energy into the overlying and underlying rocks was considered.
Bio determined the following boundaries of a low-frequency area where theoretic of results using both directions have been in a good agreement:
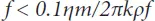
where η and ρf are, respectively, fluid viscosity and density; and k and m are rock permeability and porosity, respectively.
Sound dispersion in a micro-nonuniform medium is usually tied with the relaxation processes. These processes are leading to value leveling of some thermodynamic parameter ξ which depends on the wave pressure (or tension) in the enclosing medium and in inclusions. This leveling usually occurs through processes of heat conduction and diffusion through the surface of inclusions and is described by a relaxation time ז r. For the frequencies ω >> 1 ז r, the dispersion law may look like follows [29]:
(2.1) 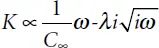
where K is the frequency limit of the sound velocity; λ is the constant depending on the difference between the sound velocity limit values at high and low frequency and on ז r; and K is the complex wave vector.
A similar dispersion law is typical also for nonuniform porous media filled with a viscous liquid due to the sound wave dispersion on the surface of nonuniformities and their conversion to rapidly fading viscous waves [28].
Let us assume that prior to the time moment t = 0, there were no wave disturbances in the medium. Then, a flat wave spreading from the side of positive x -axis values, according to the dispersion law Equation (2.1), is described by the following causal first-order wave equation:
(2.2) 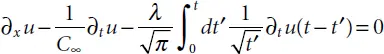
The last term in the left part of Equation (2.2)may be shown as φ 1/2( t ) * д t u ( t ), where the asterisk indicates packing of two functions and 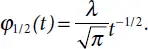
The core of the packing operator Equation (2.2)is a particular case of a more common Abel core:
(2.3) 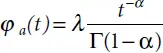
where Г is the gamma function.
The core of Equation (2.3)kind may also be used for the description of more complex media. A singular function φ α( t ) at t = 0 is integratable if 0 ˂ α ˂ 1.
Next, the authors exam the complete second order equation for flat single-dimension waves extracted from Equation (2.2)and generalized according to Equation (2.3)for mathematical modeling of wave spreading within micro-nonuniform media. The causal single-dimensional second-order wave equation is
(2.4) 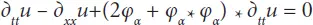
2D and 3D scalar wave equations of the medium model under review is easy to write down for an isotropic case by way of replacing the operator δ xxwith the dimension-appropriate Laplace operator. These equations obviously describe the wave spreading in some viscous-elastic medium. The right part of Equation (2.4)is different from zero at the availability of diffuse sources. The fundamental solution of Equation (2.4)must satisfy initial conditions
(2.5) 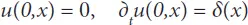
where δ ( x ) is Dirac delta function.
This fundamental solution enables the presentation of a general solution Equation (2.4)in the form of modified Duhamel integral, and in and of itself, it describes a wave impulse excited by an instantaneous point source. As Equation (2.4)is asymptotic at ω >> 1 / τ r, this model is applicable only near the wave impulse front during the time period or at a distance (C ∞ = 1) smaller than ז r(which at accepted dimensionless units equals one).
The wave impulse front that emerged at the moment t = 0 and at the point x = 0 reaches the points + x and − x at the moment t = | x |. Solution of the problem Equations (2.4)and (2.5)represents the wave after this moment if to record t = | x | + τ and 0 ˂ τ ˂ τ r=1:
(2.6) 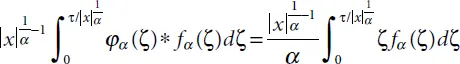
Читать дальше