Source: Copyright by Aleksandra Manecka – Padaż.

Figure 1.3 The pattern of the aluminium rest and extruded wire. The extrusion ratio equals 700.
Source: Korbel and Szyndler 2010. Copyright of Włodzimierz Bochniak.
The paper (Bochniak et al. 2006) deals with the KOBO method of forming bevel gears from structural steel. The study's subject is a single operation of complex forging on a press with the reversible rotating die displayed in Figure 1.6. Comparing the KOBO method's forging process with the conventional ones reveals that the punch pressure and temperature are considerably lower. Despite such a reduction, the products represent the die shape correctly, the structure becomes homogeneous, and the material has desired mechanical properties (see Figure 1.4) containing an example of the regular bevel gear obtained by the KOBO method from structural steel at the studied temperature of 850 °C (Bochniak et al. 2006). Let us also recall a nice illustrative picture of the bevel gear displayed on the book's cover. The image provided kindly by the editorial staff comes from other sources, and the shown example of bevel gear is the traditional milling effect.
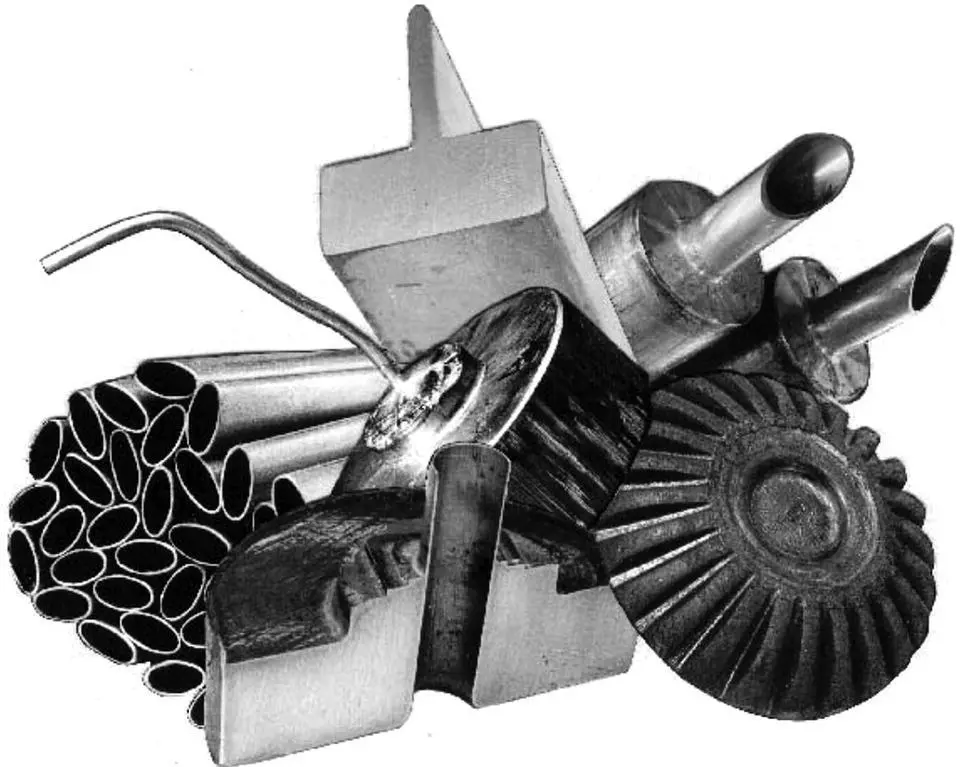
Figure 1.4 Examples of the KOBO extrusion and forging products received in semi‐industrial conditions.
Source: Korbel and Szyndler 2010. Copyright of Włodzimierz Bochniak.

Figure 1.5 Fine tube of magnesium alloy AZ91 extruded at room temperature using 1MN load capacity press.
Source: Korbel and Szyndler 2010. Copyright of Włodzimierz Bochniak.
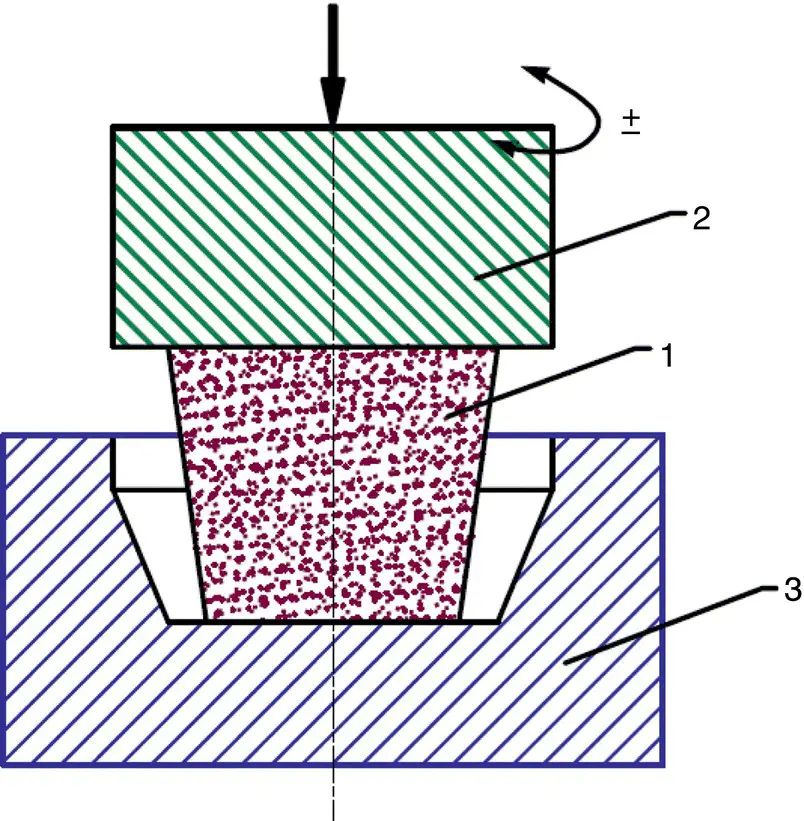
Figure 1.6 Schematic presentation of the forging process by the KOBO method: (1) forged material, (2) cyclically rotating punch, and (3) die (anvil).
Source: (Bochniak et al. 2006). Copyright by Aleksandra Manecka – Padaż.
Summing up, the authors observe the KOBO method's extrusion or forging process from the structural point of view. The slips' organisation with increasing strain leads to transgranular, localised plastic strain. Such a localisation appears as growing clusters of micro‐shear bands and is related to strain softening of metal. The rapid change of the loading scheme and corresponding change of the deformation path leads to instantaneous localisation of plastic flow in the shear bands irrespective of the deformation process's advancement. According to Korbel and Bochniak (2003), the mentioned procedure does not guarantee to keep this state for a long time, and the cyclic repetition of additional external agents in this process is required.
1.3.2 KOBO Processes Resulting in Viscous Effects
The experimental investigations and microscopic analysis of the substructure of metals and alloys carried out by Korbel and Bochniak investigation group led to the novel observation of viscous effects of deformation processes by the KOBO method. The results presented in the papers by Korbel et al. (2011), Bochniak et al. (2011, 2013) indicate that the point defects of supra‐equilibrium concentration, generated in periodically variable conditions of plastic flow in the course of the KOBO process, play a decisive role. The massive production of point defects leads to the superplastic behaviour of metallic solid not observed in other plastic‐forming methods. The authors state that: ‘It seems reasonable, therefore, to conclude that die oscillation frequency (torsion of material) is the determinant of the amount of point defects and its increase should enhance the process. The occurrence of diffusing atoms or vacancies stream equalising the concentration leads to a significant decrease in viscosity of the material, generating an alternative to the dislocation slip mechanism of plastic deformation’, cf. (Korbel et al. 2011), p. 2893. The analysis justifies the author's view that the mechanism of metal extrusion using the mentioned KOBO technology is induced by the intensive generation of point defects. Thus, the authors hypothesise that a viscous flow with ‘Newtonian fluid’ features is a dominant deformation mechanism in KOBO processes. Generally, they identify the description of deformation occurring, e.g. during extrusion by the KOBO method as viscoplastic flow. However, on the other hand, in deformable solids' mechanics, the early viscoplasticity model belongs to Bingham (1916). It shows the linear dependency of shear stress on shear strain rate:
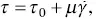
where τ 0is yield stress in shear and 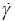 denotes the shear strain rate. Neglecting τ 0= 0, one arrives at the linear model of ‘Newtonian fluid’. An analogy with magnetorheological materials appears here. From the papers of Frąś (2015), Frąś and Pęcherski (2018), it seems that the linear Bingham model does not conform to experimental data contrary to the original nonlinear viscoplasticity model of Perzyna (1963). The similar conclusion leads the above discussion on a viscous flow resulting from the massive production of point defects activated in KOBO processes. In my view, a more comprehensive theory of the viscoplastic flow produced by shear banding is in order. The observation about the importance of viscous effects accompanying rate‐dependent plastic flow during KOBO processes is accounted for in the book.
denotes the shear strain rate. Neglecting τ 0= 0, one arrives at the linear model of ‘Newtonian fluid’. An analogy with magnetorheological materials appears here. From the papers of Frąś (2015), Frąś and Pęcherski (2018), it seems that the linear Bingham model does not conform to experimental data contrary to the original nonlinear viscoplasticity model of Perzyna (1963). The similar conclusion leads the above discussion on a viscous flow resulting from the massive production of point defects activated in KOBO processes. In my view, a more comprehensive theory of the viscoplastic flow produced by shear banding is in order. The observation about the importance of viscous effects accompanying rate‐dependent plastic flow during KOBO processes is accounted for in the book.
1.4 Summary of the Work Content
The preface introduces novel concepts and the framework of the book. Chapter 1 presents the motivation and leading thread of the work related to a detailed discussion of the physical basis developed in Chapter 2. This chapter contains the synthetic approach to observations that appear helpful in formulating the viscoplastic flow description in metallic solids produced by shear banding. These views are underlined in the text as the set of statements denoted Observations 2.1, 2.2, … 6.1, including the results of own inquiries. The heuristic foundations of the theoretical description of large inelastic deformations create the rational formulation of a multiscale system of shear bands formation. Chapter 3, on the other hand, accounts for shear banding in the continuum model of inelastic deformations. This chapter contains the results of the earlier author's investigations related to micromechanical foundations of finite plastic deformations theory accounting for the shear‐banding mechanism summarised in Observation 3.1 and Hypothesis 3.1, extending the generally accepted concept of representative volume element (RVE). The extension provides the possibility of the existence in RVE of the singular discontinuity surface of order one of the microscopic velocity field on which the tangential component of velocity experiences a jump travelling at the speed V s. Further, Chapter 4presents the basics of rational mechanics of materials. A small historical account of rational mechanics is given here. The continuum mechanics description of shear banding is the subject of Chapter 5. The theoretical foundations of the deformation of a body due to shear banding are presented in Chapter 6. In Chapter 7, the yield limit versus shear banding is considered, and, in particular, state of the art regarding the yield condition for modern materials is the subject of thorough study. Viscoplasticity models accounting for shear banding with related examples are under investigation in Chapter 8. The conclusions and remarks concerning further possible studies are provided in Chapter 9.
Читать дальше





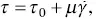
 denotes the shear strain rate. Neglecting τ 0= 0, one arrives at the linear model of ‘Newtonian fluid’. An analogy with magnetorheological materials appears here. From the papers of Frąś (2015), Frąś and Pęcherski (2018), it seems that the linear Bingham model does not conform to experimental data contrary to the original nonlinear viscoplasticity model of Perzyna (1963). The similar conclusion leads the above discussion on a viscous flow resulting from the massive production of point defects activated in KOBO processes. In my view, a more comprehensive theory of the viscoplastic flow produced by shear banding is in order. The observation about the importance of viscous effects accompanying rate‐dependent plastic flow during KOBO processes is accounted for in the book.
denotes the shear strain rate. Neglecting τ 0= 0, one arrives at the linear model of ‘Newtonian fluid’. An analogy with magnetorheological materials appears here. From the papers of Frąś (2015), Frąś and Pęcherski (2018), it seems that the linear Bingham model does not conform to experimental data contrary to the original nonlinear viscoplasticity model of Perzyna (1963). The similar conclusion leads the above discussion on a viscous flow resulting from the massive production of point defects activated in KOBO processes. In my view, a more comprehensive theory of the viscoplastic flow produced by shear banding is in order. The observation about the importance of viscous effects accompanying rate‐dependent plastic flow during KOBO processes is accounted for in the book.










