Джефф Форшоу - Квантовая вселенная. Как устроено то, что мы не можем увидеть

.

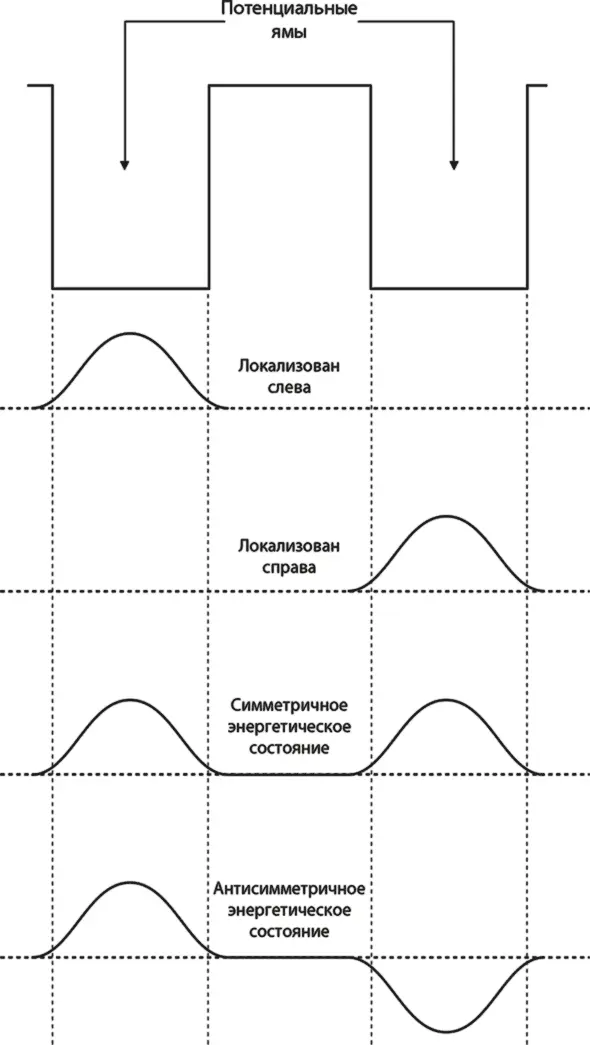
Рис. 8.1. Сверху изображен двухъямный потенциал, а снизу – четыре интересные волновые функции, описывающие электрон в этом потенциале. Только две нижние функции соответствуют электрону с определенной энергией

Наша первая задача – с помощью этой модели понять, что происходит, когда мы сводим два атома водорода: мы увидим, что, когда они в достаточной мере сближаются, образуется молекула. После этого поразмышляем над системами, состоящими более чем из двух атомов, что позволит оценить, что происходит внутри твердого тела. Если ямы очень глубоки, можно воспользоваться результатами из главы 6 и определить, чему должны соответствовать наименьшие электронные состояния. Для одиночного электрона в одиночной прямоугольной яме самое низкое электронное состояние описывается волной-синусоидой, длина которой в два раза превышает размер ящика. Следующему за ним состоянию соответствует синусоида, равная по длине размеру ящика, и т. д. Если поместить электрон в одну часть двойной ямы и если эта яма достаточно глубока, разрешенные энергии должны быть близки по значению к значениям для электрона, удерживаемого в одиночной глубокой яме, так что волновая функция будет очень напоминать синусоиду.

Однако наше внимание сейчас будет приковано к незначительным различиям между идеально изолированным атомом водорода и атомом водорода в удаленной друг от друга паре.

Можно с уверенностью ожидать, что две верхние волновые функции, изображенные на рис. 8.1, соответствуют функциям для одиночного электрона, расположенного в левой или правой яме (помните, что слова «атом» и «яма» в данном случае взаимозаменяемы). Волны – почти синусоиды, их длина равняется двойной ширине ямы. Поскольку волновые функции идентичны по форме, можно сказать, что они должны соответствовать частицам одинаковой энергии. Но это не может быть верным, потому что, как мы уже говорили, должна быть очень небольшая вероятность, что электрон может перескочить из одной ямы в другую независимо от того, насколько глубоки эти ямы и как они удалены друг от друга. Мы намекнули на эту возможность, изобразив некоторое «просачивание» волн-синусоид через стенки ямы, что отражает как раз ту незначительную вероятность нахождения ненулевых циферблатов в соседней яме.

То, что у электрона всегда есть конечная возможность перескочить из одной ямы в другую, означает, что две верхние волновые функции на рис. 8.1 не могут соответствовать электрону с определенной энергией, потому что из главы 6 нам известно, что такой электрон описывается стоячей волной, форма которой не меняется со временем, или набором циферблатов, размеры которых не меняются со временем. Если с течением времени в изначально пустой яме образуются новые циферблаты, форма волновой функции, разумеется, также изменяется. Итак, состояние определенной энергии соответствует двойной яме? Ответ таков: состояния должны быть более демократичными, выражая равную возможность обнаружения электрона в любой из ям. Это единственный способ образовать стоячую волну и не дать волновой функции метаться туда-сюда, от одной ямы к другой.

Две нижние волновые функции с рис. 8.1 как раз обладают этим свойством. Именно так и выглядят самые низкие энергетические состояния. Это единственные представимые стационарные состояния, которые выглядят как одноямные волновые функции для каждой индивидуальной ямы и при этом описывают электрон, с одинаковой вероятностью находящийся в любой из ям. Это и есть те два энергетических состояния, которые, как мы выяснили, могут присутствовать, если поместить два электрона на орбиту вокруг двух удаленных протонов и получить два почти идентичных атома водорода в соответствии с принципом Паули. Если один электрон описывается одной из двух этих волновых функций, то другой электрон должен описываться второй – так требует принцип Паули [37].

Если ямы достаточно глубоки или атомы достаточно удалены, то две энергии будут почти равны, при этом они станут почти равны самой низкой энергии частицы, удерживаемой в одиночной изолированной яме. Не нужно беспокоиться по поводу того, что одна из волновых функций словно бы встала с ног на голову: не забывайте, что при определении вероятности найти частицу в каком-либо месте значение имеет только размер циферблата. Иными словами, мы можем обратить все нарисованные в этой книге волновые функции и при этом нисколько не изменить их физического содержания. «Частично вставшая на голову» волновая функция (на рисунке она подписана как «антисимметричное энергетическое состояние») поэтому продолжает описывать равную суперпозицию электрона, удерживаемого в левой яме, и электрона, удерживаемого в правой яме. Но важно заметить, что симметричная и антисимметричная волновые функции не полностью совпадают (и не должны, а то Паули бы расстроился). Чтобы убедиться в этом, достаточно посмотреть на поведение этих двух волновых функций самой низкой энергии в области между ямами.