Маркус дю Сотой - О том, чего мы не можем знать. Путешествие к рубежам знаний

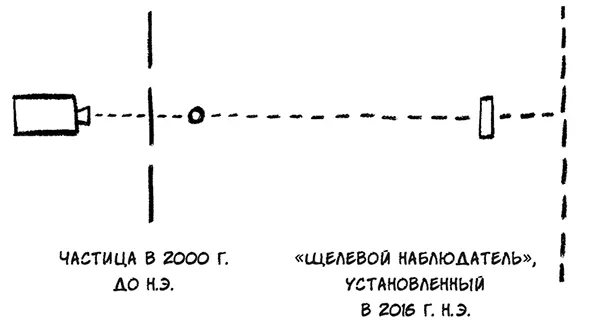
Решение об установке на пути частицы «щелевого наблюдателя», принятое в 2016 г. н. э., может изменить поведение частицы в 2000 г. до н. э.

Если мы все-таки используем «щелевой наблюдатель» много лет спустя, это будет означать, что за много лет до того электрон должен был пролететь через ту или другую щель. Но если мы не используем «щелевой наблюдатель», то много лет назад электрон должен был пролететь через обе щели. Странно, не правда ли? То, что мы делаем в начале XXI в., может изменить то, что случилось тысячи лет назад, когда этот электрон начинал свое путешествие. Создается впечатление, что существует не только множественное будущее, но и множественное прошлое, и акт наблюдения, произведенный в настоящем, может определить, что произошло в прошлом. Квантовая физика не только ставит под вопрос возможность познания будущего, но и заставляет усомниться в возможности действительного знания прошлого. Прошлое также представляется в виде суперпозиции возможностей, которые кристаллизуются только в случае наблюдения.

С моей точки зрения, интересная – и часто упускаемая из виду – особенность квантовой физики заключается в том, что вплоть до момента наблюдения она полностью детерминистична. Природа волнового уравнения, которое описывает электрон, пролетающий через щель, не вызывает никаких вопросов. Когда в 1926 г. Шредингер предложил свою теорию, он сформулировал дифференциальное уравнение, дающее полностью детерминистическое предсказание развития волновой функции. Волновое уравнение Шредингера в некотором смысле не менее детерминистично, чем уравнения движения Ньютона.

Вероятностные свойства и неопределенность возникают при попытке наблюдения частицы и извлечения классической информации. В высшей степени неклассическое и странное новое свойство заключается в этом разрывном переходе, по-видимому происходящем при «наблюдении» волны. Детерминизм внезапно исчезает, оставляя нам электрон, случайным образом расположенный в какой-то точке пространства. На большом масштабе такая случайность описывается информацией, содержащейся в волновой функции, но ученые пока не обнаружили механизма, который позволил бы определить в каждом индивидуальном случае будущее расположение электрона в конкретном эксперименте. Так ли это на самом деле? Действительно ли мы никогда не сможем определить положение электрона до наблюдения?

Когда мы производим наблюдение или измерение, происходит странный скачок, который привязывает частицу к одному определенному набору координат. Но немедленно после наблюдения эволюцию частицы начинает описывать другая волновая функция – и это положение сохраняется до следующего наблюдения и следующего скачка. Шредингеру чрезвычайно не нравились эти прерывистые изменения поведения: «Если нельзя избавиться от этих проклятых квантовых скачков, то я жалею, что вообще связался с квантовой теорией» [58].

Тут важно не переборщить с оценкой роли человека. Можно предположить, что червяки тоже могут вызывать редукцию волновой функции. И измерения могут производить не только живые существа. На другом конце потенциально безжизненной Вселенной существуют частицы, взаимодействующие с неодушевленными объектами, и в результате такого взаимодействия волновая функция редуцируется для принятия решения о свойствах частицы. Такое взаимодействие является измерением ничуть не меньше, чем наши экспериментальные исследования в лаборатории. Вселенная заполнена излучением, которое освещает все, что оно встречает на своем пути. Может быть, именно поэтому Вселенная в целом кажется классической, а не пребывающей в постоянном состоянии неопределенности? Это предположение связано с концепцией, которую физики называют декогеренцией.

Мне очень трудно уместить в голове идею о том, что наблюдение становится точкой раздела между детерминистическим электроном, описываемым волновой функцией, и электроном, внезапно получающим точное, но абсолютно случайно определенное местоположение. Вся эта история кажется совершенно безумной. Тем не менее нельзя не признать, что она успешно работает в качестве инструмента для вычислений. Рассказывают, что физик Дэвид Мермин говорил тем, кого, как и меня, беспокоила такая неизвестность, «заткнитесь и считайте». По тому же принципу теория вероятностей применяется к броску игральной кости. Хотя движением кости управляют уравнения Ньютона, лучшим средством для вычисления ее возможного поведения остается теория вероятностей.