Маркус дю Сотой - О том, чего мы не можем знать. Путешествие к рубежам знаний

Появление чудес в случайном процессе удобно рассмотреть на примере лотереи. 6 сентября 2009 г. в болгарской государственной лотерее выиграли следующие номера:

4, 15, 23, 24, 35, 42.

Четыре дня спустя выпали те же шесть номеров. Казалось бы, невероятное событие. Болгарское правительство тоже так решило и немедленно назначило расследование возможной коррупции. Однако правительство не учло того, что по всей планете каждую неделю проводится множество разных лотерей. Их проводят многие десятилетия. Если посчитать, получится, что удивляться скорее следует отсутствию таких поразительных на первый взгляд результатов.

Тот же принцип действует и в отношении условий возникновения самовоспроизводящихся молекул в первичном бульоне, из которого состояла Земля до появления жизни. Стоит смешать достаточно большое количество водорода, воды, углекислого газа и некоторых других органических газов и подвергнуть их воздействию молний и электромагнитного излучения – и даже в лабораторном опыте можно наблюдать возникновение органических материалов, встречающихся только в живых существах. Никому не удалось добиться самопроизвольного возникновения в лабораторных условиях чего-либо столь необыкновенного, как ДНК. Вероятность такого явления крайне мала.

Но в том-то и дело, потому что с учетом существования во Вселенной миллиарда миллиардов – или около того – планет, пригодных для проведения такого эксперимента, и наличия приблизительно миллиарда лет на его проведение было бы более удивительно, если бы такая предельно малая вероятность возникновения чего-то подобного ДНК не осуществилась. Бросая 36 игральных костей в течение миллиарда лет на миллиарде миллиардов разных планет, наверняка можно получить один бросок, в котором на всех 36 костях выпадут шестерки. А уж дальше полученная самовоспроизводящаяся молекула будет способна размножаться самостоятельно, так что для запуска эволюции необходима всего одна счастливая случайность.

Проблема человека в отношении оценки вероятности чудес – таких как возникновение жизни – состоит в том, что наш разум плохо приспособлен для обращения с очень большими числами. Поэтому наши интуитивные представления о вероятности хромают.

Однако в эволюции действует не только математика вероятностей. Дерево эволюции само по себе обладает одним интересным качеством, делающим его сходным с формами, возникающими в теории хаоса; это качество называется фрактальностью.

Дерево эволюции дает картину развития жизни на Земле. Продвижение по нему соответствует продвижению во времени. Каждое ответвление дерева означает развитие нового вида. Если ветвь заканчивается, это означает вымирание данного вида. Природа дерева такова, что его общая форма, как кажется, повторяется все в меньшем и меньшем масштабе. В этом и состоит характерная черта объектов, которые математики называют фракталами. В увеличенном виде любая малая часть дерева выглядит поразительно похожей на более крупные его структуры. Такое самоподобие означает, что понять, на каком масштабе мы рассматриваем дерево, очень трудно. Такова классическая особенность фрактала.

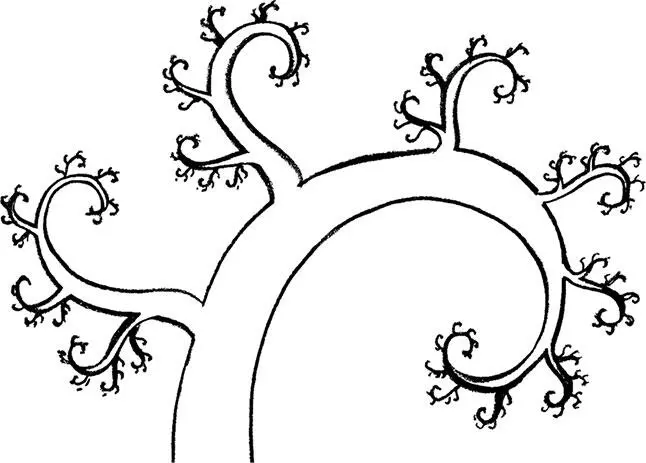
Фрактальное дерево эволюции

Фракталы обычно бывают геометрической визитной карточкой хаотических систем, так что наличие такой структуры говорит о том, что в эволюции работает динамика хаоса: малые изменения генетического кода могут порождать огромные расхождения результатов эволюции. Такая модель не обязательно противоречит идее конвергенции, поскольку даже в хаотической системе остаются точки, к которым стремится развитие модели. Такие точки называются аттракторами. Но она несомненно ставит под вопрос возможность воспроизведения того, что мы имеем сейчас на Земле, в случае повторного проведения эволюции. Биолог-эволюционист Стивен Джей Гулд утверждает, что, если заново проиграть ленту эволюции, результаты ее будут сильно отличаться от существующих. Этого обычно и ожидаешь от хаотической системы. Как и в случае погоды, чрезвычайно малые изменения начальных условий могут привести к разительно отличающемуся исходу.

Кроме того, Гулд ввел в оборот идею прерывистого равновесия, которая отражает тот факт, что биологические виды, судя по всему, остаются неизменными в течение долгих периодов, после чего с ними происходят кажущиеся чрезвычайно быстрыми эволюционные изменения. Было показано, что эта черта также характерна для хаотических систем. Наличие влияния хаоса на эволюцию выражается в том, что многие вопросы эволюционной биологии вполне могут оказаться среди того, чего мы не можем познать, из-за их связи с математикой хаоса.