Артур Бенджамин - Магия математики - Как найти x и зачем это нужно

Теорема:Если число 2 n – 1 является простым, число 2 n–1× (2 n – 1) будет совершенным.

Доказательство:Допустим, что число p = 2 n – 1 – простое. Докажем теперь, что число 2 n–1 p – совершенное. Какие величины являются его собственными делителями? Сначала – делители, которые не используют множитель p : 1, 2, 4, 8…., 2 n–1. Все они сводятся к сумме 2 n – 1 = p . Потом – все остальные (за исключением самого 2 n–1 p ), которые включают в себя множитель p и которые дают в сумме p (1 + 2 + 4 + 8 +… + 2 n–2) = p (2 n–1 – 1). Следовательно, общая сумма всех собственных делителей составит

что и требовалось доказать.

Великий Леонард Эйлер доказал, что каждое четное совершенное число может быть сведено к этой форме. Именно это представление помогло определить 48 совершенных четных чисел. Существуют ли в принципе среди совершенных чисел нечетные, не знает никто. Доказано, что если и существуют, то наименьшее из них состоит из более чем трех сотен цифр. Не существование же их пока что так и не доказано.

С простыми числами связано множество нерешенных математических проблем. Одну из них я уже упоминал: неизвестно, бесконечно ли количество простых чисел Фибоначчи (если помните, мы выяснили, что во всей последовательности всего лишь два полных квадрата чисел – 1 и 144 – и столько же кубов – 1 и 8).

Еще одна проблема – известная как гипотеза Гольдбаха – основана на предположении, что любое четное число больше 2 есть сумма двух простых чисел. Доказать этого никто не смог, однако известно, что, если контрпример и существует, в нем должно быть никак не меньше 19 цифр. (Совсем недавно, в 2013 году, в решении очень похожей проблемы произошел прорыв: перуанец Харальд Хельфготт доказал, что любое нечетное число больше 7 есть сумма как максимум трех нечетных простых чисел.)

А еще есть простые числа-близнецы (парные простые числа) – простые числа, разность между которыми составляет ровно 2: 3 и 5, 5 и 7, 11 и 13, 17 и 19, 29 и 31 и так далее. Единственные «тройняшки» в этом ряду – это 3, 5 и 7. И хотя было доказано (в качестве частного случая теоремы Густава Дирихле [18], что количество простых чисел, заканчивающихся на 1 (а также на 3, 7 или 9), бесконечно, вопрос о том, бесконечно ли количество простых чисел-близнецов, остается открытым.

Закончить эту главу я бы хотел доказательством, которое может показаться вам притянутым за уши (да что уж греха таить, именно за уши оно и притянуто). Тем не менее смею надеяться, что оно вас все-таки удовлетворит.

Утверждение:Все положительные целые величины интересны.

Доказательство:Вы, без сомнений, согласитесь, что первые положительные числа не оставляют вас равнодушными. Например, 1 – это самое первое положительное число, 2 – первое четное положительное число, 3 – первое нечетное простое число… Предположим обратное – что совсем не все числа так уж интересны. Тогда есть некая самая первая навевающая скуку величина. Назовем ее N . Но разве самого этого факта недостаточно, чтобы сделать N отличной от всех остальных величин и хотя бы уже поэтому интересной? И разве не доказывает это, что «скучных» чисел попросту не бывает?

Начнем, пожалуй, с одной геометрической задачки, которая вполне сойдет за фокус. Возьмите листок бумаги и сделайте следующее.

Шаг 1. Начертите фигуру из четырех не пересекающихся друг с другом линий. Должен получиться четырехугольник. Подпишите углы по часовой стрелке литерами A, B, C и D . Вот несколько возможных примеров:

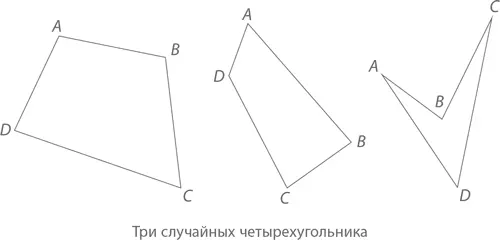
Шаг 2. Отметьте центральные точки сторон AB, BC, CD и DA буквами E, F, G и H соответственно.

Шаг 3. Соедините эти точки пунктирными линиями так, чтобы получился еще один прямоугольник, EFGH , вот так:

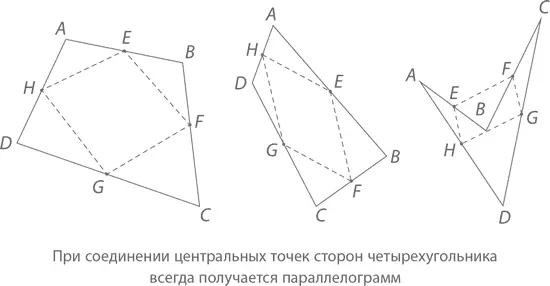
Хотите – верьте, хотите – нет, но он всегда будет параллелограммом. Другими словами, линия EF будет параллельна линии GH , а линия FG – линии HE (при этом сторона EF будет той же длины, что и сторона GH , а сторона FG – той же длины, что и сторона HE ). На рисунках выше это отлично заметно, но мне очень хочется, чтобы вы сами все это начертили.