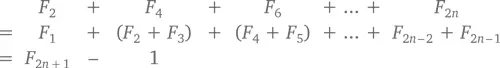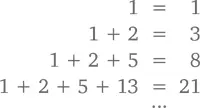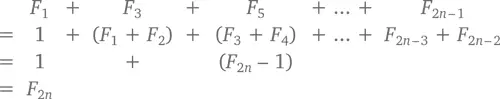В целом, если мы будем исходить из того, что F 2= F 1= 1, и заменять каждое последующее число суммой двух предыдущих, мы увидим, что нужную нам сумму можно легко свести к сумме первых 2 n – 1 чисел последовательности.
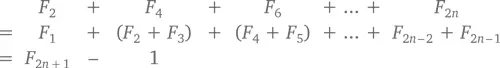
А теперь давайте посчитаем сумму первых n чисел, занимающих нечетные позиции.
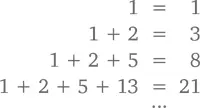
Здесь все еще проще, как ни странно. Сумма n чисел, занимающих нечетные позиции в последовательности, – это просто следующее число Фибоначчи. Представить это можно следующим образом:
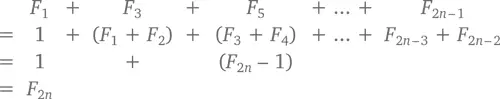
Отступление
К ответу можно прийти и другим способом – с помощью того, о чем мы только что говорили. Если мы вычтем первые n чисел, стоящих в последовательности на четных позициях, из первых 2 n чисел, получатся первые n чисел, находящиеся на нечетных позициях:
F1 + F3 + F5 +… + F2n– 1
= ( F1 + F2 + … + F2n – 1 ) – ( F2 + F4 +… + F2n – 2 )
= ( F2n + 1 – 1) – ( F2n – 1 – 1)
= F2n
Подсчет с помощью чисел Фибоначчи
Мы заглянули лишь в замочную скважину той двери, за которой раскинулся сад самых настоящих чудес. Только растут в нем не деревья, а числовые закономерности, уходящие корнями в последовательность Фибоначчи. И вам, наверняка, не терпится узнать, для чего еще, кроме подсчета поголовья кроликов, нужны эти числа. На самом деле – много для чего. В 1150 году (задолго до того, как Леонардо Пизанский представил миру задачку про кроликов) индийский поэт Хемачандра задался очень интересным вопросом: сколькими способами можно сложить стихотворную стопу из n безударных или ударных слогов. Давайте сперва переведем эту проблему из плоскости поэзии в плоскость математики.
Вопрос: Сколькими способами можно записать число n как сумму единиц и двоек?
Ответ: Обозначим результат как f n . Вот что будем иметь при стартовых значениях n :

У нас есть один вариант, дающий в сумме 1, два варианта, дающих 2 (1 + 1 и 2), и три варианта, дающих 3 (1 + 1 + 1, 1 + 2 и 2 + 1). Повторимся: для получения нужной нам суммы доступны только единицы и двойки. При этом порядок этих цифр имеет значение: 1 + 2 и 2 + 1 суть две разные комбинации. Получить 4 можно уже пятью разными вариантами: 1 + 1 + 1 + 1, 1 + 1 + 2, 1 + 2 + 1, 2 + 1 + 1, 2 + 2. По всему выходит, что числа в правой части нашей таблицы – это числа из последовательности Фибоначчи, и так оно есть на деле.
Давайте попробуем понять, почему вдруг 5 можно получить f 5 = 8 различными способами. Начинаться сложение может с 1 или 2. Сколько вариантов будет начинаться именно с 1? За первой цифрой должна следовать некая комбинация 1 и 2, которая в сумме даст 4, а по предыдущей строке мы знаем, что таких комбинаций у нас f 4= 5. Теперь так же посчитаем, сколько вариантов будет начинаться с 2. В этом случае комбинация после первой цифры должна давать нам 3. Смотрим чуть выше по таблице и видим, что f 3= 3. Значит, общее количество комбинаций 1 и 2, дающих в сумме 5, должно быть 5 + 3 = 8. Тот же алгоритм приведет нас к тому, что для 6 таких комбинаций будет 13: f 5= 8, начинающихся с 1, плюс f 4= 5, начинающихся с 2. В целом же, для суммы n их число равно f n, из которых f n –1имеют в начале 1, а f n –2 – 2. Следовательно,
fn = fn – 1 + fn – 2
Причем все значения f nдублируют числа последовательности Фибоначчи и будут и дальше их дублировать с увеличением значения n . Причина в том, что это и есть последовательность Фибоначчи, только в несколько измененном виде – с небольшим смещением . Обратите внимание, что f 1= 1 = F 2, f 2= 2 = F 3, f 3= 3 = F 4и т. д. (для удобства договоримся, что f 0= F 1= 1, а f –1= F 0= 0). Обобщая, мы можем утверждать, что при n ≥ 1
Читать дальше
Конец ознакомительного отрывка
Купить книгу