Марио Ливио - φ – Число Бога. Золотое сечение – формула мироздания

Современные физические теории, нацеленные на объяснение существования всех элементарных (субатомных) частиц и основных взаимодействий между ними, также основаны на математической симметрии и в этом смысле очень похожи на теорию Кеплера, который опирался на симметричные качества платоновых тел, дабы объяснить количество и свойства планет. У модели Кеплера была еще одна общая черта с современной фундаментальной теорией Вселенной: обе теории по своей природе редукционистские , то есть они стремятся объяснить много явлений малым количеством физических законов. Например, модель Кеплера выводит и количество планет, и свойства их орбит из платоновых тел. Подобным же образом современные теории – например, теория струн – опирается на основополагающие сущности (струны), очень маленькие (более чем в миллиард миллиардов раз меньше атомного ядра), из которых выводятся все свойства элементарных частиц. Струны – подобно скрипичной струне – вибрируют и порождают разнообразные «тоны», и все известные элементарные частицы всего-навсего воплощают эти тоны.

Во время пребывания в Граце Кеплер интересовался золотым сечением, что привело к другому интересному результату. В октябре 1597 года ученый написал своему бывшему учителю Местлину о следующей теореме: «Если на отрезке, разделенном в крайнем и среднем отношении, построить прямоугольный треугольник так, чтобы прямой угол лежал на перпендикуляре, проведенном в точке разделения, то меньший катет будет равняться большему сегменту разделенного отрезка». Чертеж к этой теореме представлен на рис. 61. Отрезок АВ разделен точкой С в золотом сечении. Кеплер строит прямоугольный треугольник ADB с гипотенузой АВ так, что прямой угол D лежит на перпендикуляре, проведенном из точки золотого сечения С. Затем он доказывает, что BD (короткий катет прямоугольного треугольника) равен АС (более длинному сегменту отрезка, разделенного в золотом сечении). Кроме применения золотого сечения, такой треугольник примечателен еще и тем, что исследователь пирамид Фридрих Ребер в 1855 году приводит его при доказательстве одной из ложных теорий, предполагавших применение золотого сечения при строительстве пирамид. О трудах Кеплера Ребер не знал, однако применил похожее построение, чтобы подтвердить свое мнение о важнейшей роли «божественной пропорции» в архитектуре.

Публикация « Mysterium Cosmographicum » стала поводом для знакомства Кеплера с Тихо Браге; местом встречи, состоявшейся 4 февраля 1600 года, стала Прага, в то время – резиденция императора Священной Римской Империи. В итоге этой встречи в октябре того же 1600 года Кеплер перебрался в Прагу и стал помощником Тихо Браге (из-за своей лютеранской веры он был вынужден покинуть католический Грац). После смерти Браге 24 октября 1601 года Кеплер стал придворным математиком.

Тихо оставил массу наблюдений, в особенности связанных с орбитой планеты Марс, и Кеплер, опираясь на эти данные, открыл первые два закона движения планет, названные его именем. Первый закон Кеплера гласит, что орбиты известных планет вокруг Солнца – не окружности, а эллипсы с Солнцем в одном из фокусов (рис. 62; для наглядности эллипс вытянут гораздо сильнее, чем на самом деле). У эллипса есть две точки, так называемые фокусы, такие, что сумма расстояний любой точки эллипса до обоих фокусов всегда постоянна. Второй закон Кеплера утверждает, что планета движется быстрее всего, когда она ближе всего к Солнцу (эта точка называется перигелий), а медленнее всего – в самой дальней точке (афелии), так что линия, соединяющая планету с Солнцем, описывает (заметает) равные площади за равные промежутки времени (рис. 62). Вопрос о том, благодаря чему законы Кеплера справедливы, был главной нерешенной загадкой науки почти семьдесят лет после того, как Кеплер опубликовал свои законы. Понадобился гений Исаака Ньютона (1642–1727), чтобы сделать вывод, что планеты держатся на орбитах благодаря силе тяготения. Ньютон объяснил законы Кеплера при помощи уравнений, где законы, описывающие движение тел, сочетались с законом всемирного тяготения. Он показал, что эллиптические орбиты с переменной скоростью (согласно законам Кеплера) и предоставляют собой единственное возможное решение этих уравнений.

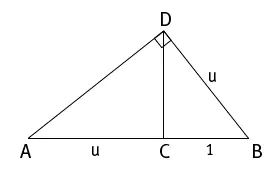
Рис. 61

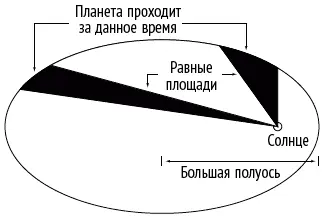
Рис. 62