И. Пименов - Мир приключений, 1928 № 08

Можно еще решить арифметически, исходя именно из первого условия, т. е. из последней приведенной формулы. Нетрудно убедиться, что число 104 нельзя разбить ни на какие иные 3 или 2 квадрата чисел (меньших 10 каждое), кроме приведенных выше цифр 8, 6 и 2. Расстановка этих трех цифр в искомое число легко делается при сопоставлении с 2-м и 4-м условиями задачи.

В оценке этой задачи, за всестороннее освещение ее, некоторым участникам конкурса было зачтено вместо 3 очков по 4.

Надо решить три помещенных здесь задачи №№ 21, 25 и 26. Качество решений оценивается очками, согласно указаний в заголовках самих задач. Еще полочка может быть прибавлено дополнительно за тщательность и аккуратность в выполнении решений, — при соблюдении, конечно, всех требуемых условий. Те участники конкурса, которые соберут в сумме наибольшее число очков, премируются следующими 10 премиями (при равенстве очков вопрос решается жребием):

1-я премия.«Лис Патрикеевич» — Гёте, большой том с 66 эстампами на меди и 21 гравюрами (ценность — 15 руб.).

2-я премия.Бесплатное получение в течение 1928 года журнала «Вестник Знания».

3-я премия. Грез — художественное издание с красочными иллюстрациями.

4-я премия. «Гений и творчество» — проф. Грузенберга — основы теории и психологии творчества.

5-я—10 премии. По выбору премированных одно из след. изданий: «Наука в вопросах и ответах», «Общественная медицина и социальная гигиена» — проф. З. Г. Френкель, «Пылающие бездны» — фантаст. роман Н. Муханова или шесть. №№ «Мир Приключений» за 1926 или 1927 г. г.

Все решения по конкурсу должны быть изложены на отдельном листе, сверху коего должны быть указаны фамилия, адрес и № подписного билета (или взамен того наклеен адрес с бандероли, под которой получается журнал). На конверте нужно делать надпись «В отдел задач».

Срок присылки решений — 25 октября с. г.

Трапеция с секретом.

Задача № 24 — до 4 очков.

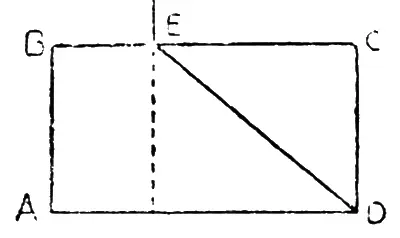
Возьмите любой прямоугольник, напр., ABCD (см. чертеж) и отрежьте от него уголок CED так, чтобы при подвеске оставшейся фигуры (трапеции ABED) на ниточке за точку Е основания этой трапеции AD и BE остались-бы перпендикулярными к отвесной нити. Второй вопрос: как изменится решение задачи, если взятый прямоугольник вытянуть или сжать по высоте его, сохранив прежнее основание ВС

Можно-ли угадать?

Задача № 25 — 2 очка.

Вам говорят, что задуманное число при делении на некоторый целый делитель дает частное А, а при делении на какой-то другой делитель дает частное В. Можно-ли и в каких именно случаях узнать задуманное число, если вам назовут оба частных А и Б?

Юбилейный акростих.

Задача № 26 — до 3 очков.

Подберите семь таких слов, которые при написании их столбцом одно под другим (буква под буквой) дадут прочесть в двух буквенных вертикалях, — с одной сверху вниз, а в другой снизу вверх, — фамилии двух классических русских писателей, юбилеи коих мы справляем в этом году. Подбираемые слова должны быть именами существительными нарицательными (в единств. числе, именит. падеже; и но возможности из одинакового числа букв.

Чей план?

Задача № 16.

Как и при всяком передвижении, наибольшее усилие от паровоза требуется в первые моменты, когда нужно сдвинуть поезд с места и когда он еще не приобрел достаточной скорости. Естественно, что именно в эти моменты жел. дор. путь должен быть наиболее удобно-проходимым, т. е. должен представлять меньше всего сопротивлений: ясно, что прямой участок пути будет для этой цели более подходящим, чем участок с кривыми. Значит, верхний путь будет служить для движения вправо, а нижний — для движения влево. И, значит, такой разъезд не может находиться в пределах СССР, так как здесь движение происходит по левой колее.

Несколько откликнувшихся читателей дали ответы неверные. Правильно решил П. Б. Горцев (Ростов).

Пойманный вор.

Задача № 17.

1) Шарики не могут быть слишком крупными, чтобы вся урна не занимала много места, но и не должны быть мелкими, чтобы было заметно, если кто-нибудь достанет из урны одновременно более одного шарика. Пожалуй, удобнее всего размеры некрупной сливы.