Николай Морозов - Стихотворения

Но, даже и при значительной частоте повторения некоторых служебных частиц речи, могут обнаруживаться, как мы уже видели у Толстого, значительные колебания их числа в различных произведениях того же самого автора, если мы будем брать всего лишь тысячу слов. Образчиком такого неопределённого спектра является, между прочим, и приводимый мною на рис. 32, где я сопоставил отрицательную частицу не с союзом и , в его двух вариациях: первая (и') соединяет между собою существительные или прилагательные имена, вторая (и") – глаголы или пелые фразы. Мы видим, что колебания их числа в различных произведениях у того же самого автора настолько же резки, как и у двух различных писателей. Однако и тут могут найтись авторы, у которых этот спектр обнаружит явное постоянство во всех произведениях.

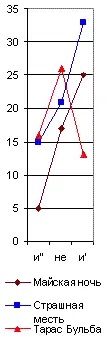
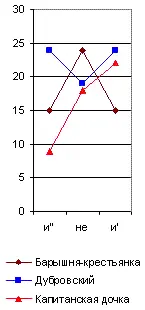
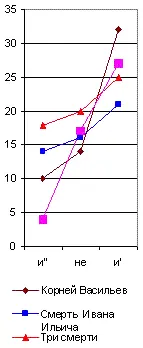
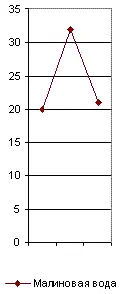
Рис. 32. Спектр и"-не-и'.

Все лингвистические спектры, где, как у предыдущих, лишь высчитывается прямое среднее число той или другой служебной частицы на тысячу слов, можно назвать естественными . Они не всегда удобны для наглядного выражения слоговой физиономии автора и, кроме того, с ними надо уметь обращаться при их подборе для спектра. Составьте, например, спектр из каких-либо двух часто употребляемых служебных частиц и из одной мало употребительной. Поставив её на графике в середине между двумя первыми, вы получите всегда фигуру в роде V , в которой сольются все индивидуальные особенности слога различных авторов. Но особенности каждого из них станут ясно определёнными, когда мы расположим все такие частицы не в случайном порядке, а по мере уменьшения или по мере увеличения их средней употребимости у писателей данной эпохи. Так я и сделал в предыдущих таблицах, иначе мои графики обнаружили бы лишь ложное сходство.

Чтобы избежать подобных фикций, при дальнейшем развитии предлагаемого мною метода следует все естественные спектры обращать в приведённые . Для этого надо только соблюдать следующее правило.

Среднее число повторений каждой служебной частицы на тысячу слов данного произведения нужно разделить на среднюю повторяемость той же частицы, вычисленную по многим авторам данной эпохи. Тогда вместо предыдущих абсолютных цифр получатся Коэффициенты индивидуальности авторов, величиною своею то более , то менее единицы. Изобразив для их представления на графике единицу высоты горизонтальной линией ( рис. 33) и обозначив выше её избыток исследуемой частицы в десятых долях единицы, а ниже недочёт (в таких же долях), мы и получим приведённые спектры . Образчик их я дал здесь на рис. 33 для спектра из предлогов в, на и с , который в естественном виде был показан уже ранее, на рис. 29.

Составил я его так. Определив среднюю повторяемость этих трёх предлогов на тысячу слов по приведённым в примечании десяти произведениям Пушкина [7], Гоголя и Толстого, я получил знаменатели однородности для этих предлогов. Именно:

для В ………. 26

для НА ……… 20

для С ………. 11

Здесь предлоги в, на и с написаны надстрочными буквами в знак того, что они не относятся к какому-либо отдельному автору, а представляют собой обобщённые величины . Разделив на них число повторений тех же самых предлогов (найденных среди тысячи же слов) в отдельных произведениях Гоголя, Пушкина и Толстого, мы получаем результаты, приведённые на таблице XIII.

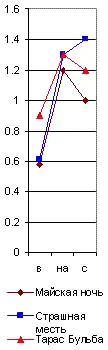
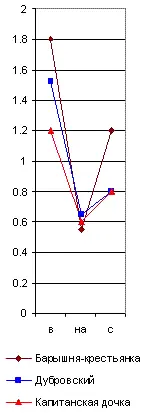
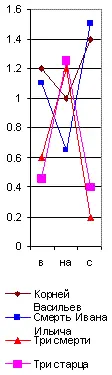
Рис. 33. Приведённый спектр предлогов в-на-с.

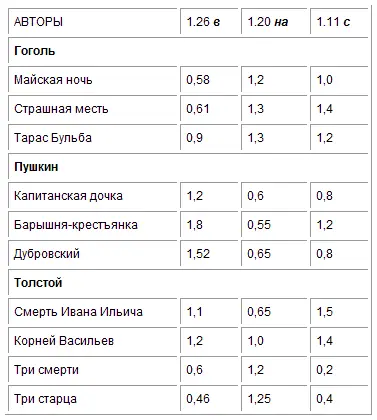
Перенеся это на графику, мы и находим для указанных произведений главный предложный приведённый спектр ( рис. 33). В нём оказываются исключёнными все ложные сходства, зависящие от случайных группировок между собой исследуемых служебных частиц речи, а остаются только одни действительные сходства или различия.