Егор Кизим - Овощи души

Пример № 1

Пятый постулат Евклида гласит, что через точку вне прямой можно провести лишь одну прямую, параллельную данной.

Две параллельные прямые (а и Ь) задают на плоскости основание трапеции с произвольно выбранными двумя другими сторонами (с и d). Прямые а и b аналогичны двум противоположностям в законе единства и борьбы противоположностей.

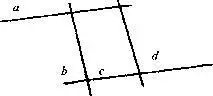
По другому обстоит дело с постулатом Римана: через точку вне прямой нельзя провести ни одной прямой, параллельной данной. Получается, что на Римановой поверхности принципиально невозможно построить даже основание трапеции, так как оно образуется двумя параллельными прямыми а и Ь, аналогичными двум противоположностям, следовательно закон единства и борьбы противоположностей на римановой поверхности принципиально невыполним, его просто не существует!

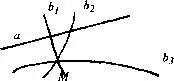
С постулатом Лобачевского происходят иные курьезы: через точку вне прямой можно провести бесчисленное множество прямых, параллельных данной. Выходит, что на поверхности Лобачевского принципиально допустимо построить множество оснований трапеции, у которых одна из прямых будет общей, а других прямых, параллельных данной и имеющих одну общую точку будет множество, следовательно закон единства и борьбы двух противоположностей на поверхности Лобачевского трансформируется в закон единства и борьбы множества противоположностей.

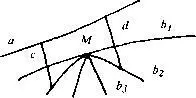
Теория относительности утверждает, что реальное пространство, в котором мы имеем счастье проживать, по сути своей является неевклидовым, но наши органы чувств чаще всего не могут уловить пространственно–временной кривизны, поэтому закон единства и борьбы двух противоположностей, который так отчаянно полюбили марксисты всех мастей, до некоторой степени отражает лишь чувственное восприятие реальных образований, видимость и кажимость чего‑либо, но не способен описывать объективный ход вещей в достаточной степени приближения, достаточной, чтобы не впадать в ошибочные социологические и естественно–научные теории.

Пример № 2

Представьте гипотетическую ракету, в которой покоится лоренцовский стержень вдоль направления ее движения. Теория относительности утверждает, что при движении будет происходить сокращение длины стержня. При скорости, равной скорости света, концы стержня А и В сократятся настолько, что сольются друг с другом (явление сингулярности). Но совпадут не только концы стержня (его противоположности), но и его индифферентное место X, взятое произвольно между концами А и В.

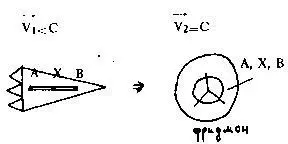
А совпадет с X, А противоположно В, следовательно X противоположно В;

В совпадет с X, В противоположно А, следовательно X противоположно А;

Поэтому А, X, В являются противоположностями, треугольником противоположностей. Но место X выбрано на лоренцевском стержне произвольно, таких мест может быть множество, следовательно при скорости равной скорости света у предмета или явления появляется множество противоположностей.

Если принять во внимание гипотезу академика Маркова, который полагает, что элементар–ными частицами нашего трехмерного мира являются «высовывающиеся» в нашу метагалактику сечения огромных четырехмерных сфер — вселенных, то получится, что наш объективный мир, построенный из таких четырехмерных субмикрочастиц, должен подчиняться законам этого четырехмерно–пространственного мира (например, закону «четвертое не есть»).

Данный закон описывает пространственно-временные отношения следующим образом: длина, ширина, высота и время — первое, второе, третье и четвертое (соответственно); отрицание четвертого (времени) есть фридмонность — некое надтрехмерно–пространственно–временное образование, влияющее на всех и вся в нашем мире, но до сих пор не познанное.

Вообще для неевклидова пространства–времени, с его искривленной структурой, понятие 2–х противоположностей противоестественно. Стержень ABC в таком пространстве искривляется. В результате чего становятся противоположностями индифферентное место В и концы стержня А и С. Однако «плоскатики» (Ф. Ю. Зигель), живущие в границах этой плоскости, не заметят, что стержень ABC сам себя пересекает в точках А и С. В объективном мире так и происходит, поэтому — и только поэтому противоположные стороны одного явления, процесса имеют сходство, обусловленное общностью координат.